[Kernel-based Learning] Support Vector Machine (SVM) - Linear & Hard Margin

본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다

Linear Classification

SVM (Support vector Machine)은 binary classifier를 만드는 것이 목적이다. 각 알고리즘마다 분류를 만드는 절차가 다르기 때문에 아래 예시와 같이 경계면의 형태가 다르다.

우리가 아는 NN은 비선형 분류다. 오늘 알아볼 SVM은 기본적으로 선형 모형이다.

$$ S=((x_{1} ,y_{1}), ..., (x_{n}, y_{n}))\in X \times \{-1,+1\} $$

학습 데이터 $X$는 i.i.d.이고, 샘플링 되었다고 가정한다. 우리는 $n$개의 데이터 셋을 가지고 있고, binary classification이기 때문에 $-1, +1$로 지정한다. logistic regression에서는 binary classification에서 0과 1로 표현을 하는데 SVM에서는 $-1, +1$로 설정한다. 이렇게 하는 이유는 수학적으로 계산을 더욱 간편하게 하려고 하는 것이다. 큰 문제는 없다. 자세한 것은 뒤에서 설명하겠다.

우리의 목적은 주어진 조건에서 hypothesis $h: X\rightarrow \{-1, +1\}$를 찾는 것이다. 여기서 hypothesis는 model라고 생각하면 되고, $X$라는 공간에서 매칭 되는 정답으로 가는 좋은 성능의 model을 찾는 것이다.

좋은 성능의 model은 small generalization error를 찾는 것이다.

Classifier는 2차원 공간 상에서는 1차원 직선을 사용하고, 3차원에서는 면을 통해 구분한다.

따라서 우리의 최종 목적은 d-dimension에서 두 범주를 잘 구분하는 $d-1$ dimension의 hyper plane을 찾는 것이다.

$$ H=\{\mathbf{x} \rightarrow sign(\mathbf{w}\cdot \mathbf{x}+b:\mathbf{w}\in R^{d}, b \in R\} $$

Binary classification의 기본적인 hypothesis는 위와 같이 정의 된다. $\mathbf{w}\cdot \mathbf{x}+b$를 통해 값을 계산하고, 이 값을 $sign$을 통해 +1, -1로 분류한다.

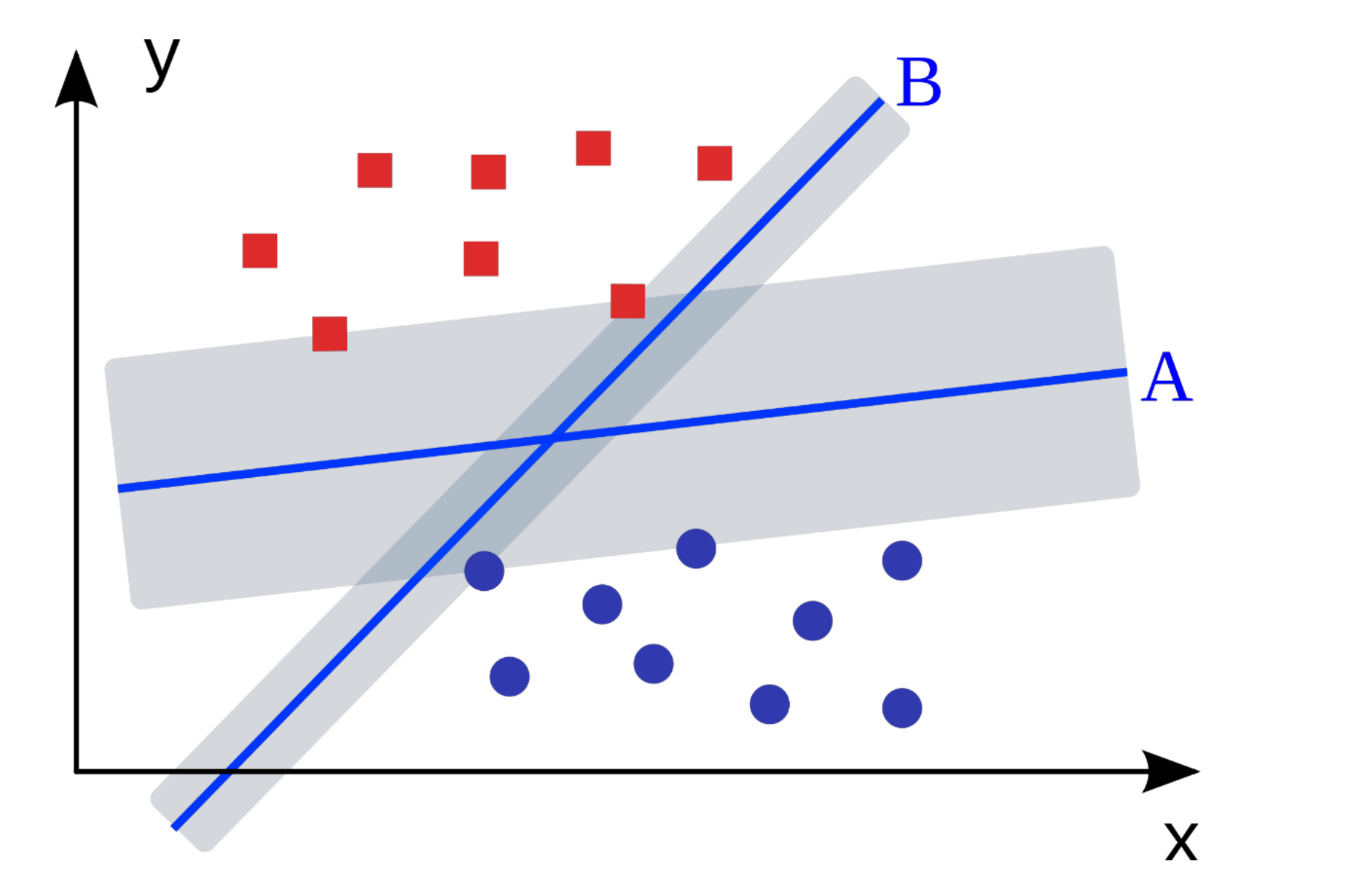
위 그림에서 $A$와 $B$ 중 어떤 분류기가 더 좋을까?

둘 다 잘 분류하고 있는 모습을 보인다. 이전 포스트에서 $R =R_{emp}+capacity$로 성능을 측정한다.

$A,B$는 둘 다 $R_{emp}=0$ 이지만 capacity term은 달라진다.

여기서 SVM이 선호하는 것은 $A$ 분류기이다. 그 이유는 지금 현재 shading이 되어 있는 회색 부분을 margin이라고 부른데, 이는 분류 경계면부터 등간격으로 확장시켰을 때, 가장 가까운 양 쪽 범주의 객체들 간의 거리이다.

이 margin이 클수록 capacity term이 줄어든다. 따라서 $A$를 선호하게 된다.

우리의 핵심은 margin은 최대화하는 것이다.

과거에는 인공 지능이 local optimum이 많아 빠져나오기 힘들 것이라고 생각했다. 그래서 이 중에 무엇을 하든 간에 인공 지능은 indifferent 하다고 생각했다. 이러한 문제점을 해결하기 위해 SVM은 global optimum을 찾는 것이 핵심이었다.

하지만 인공 지능의 경우 현재로서는 local optimum을 빠져나오는 방법이 존재하였다. 이를 다른 말로 하면 모든 방향으로 gradient가 0인 경우는 거의 없었다. 특정한 쪽으로는 0일 때가 존재했지만, 이를 수많은 학습을 통해 global optimum에 도달할 수 있었다.

이 실험 결과 이후로 인공 지능의 성능이 SVM을 넘어섰다.

SVM의 성능을 올리기 위해서는 margin을 올려야 한다. Margin을 어떻게 계산할까?

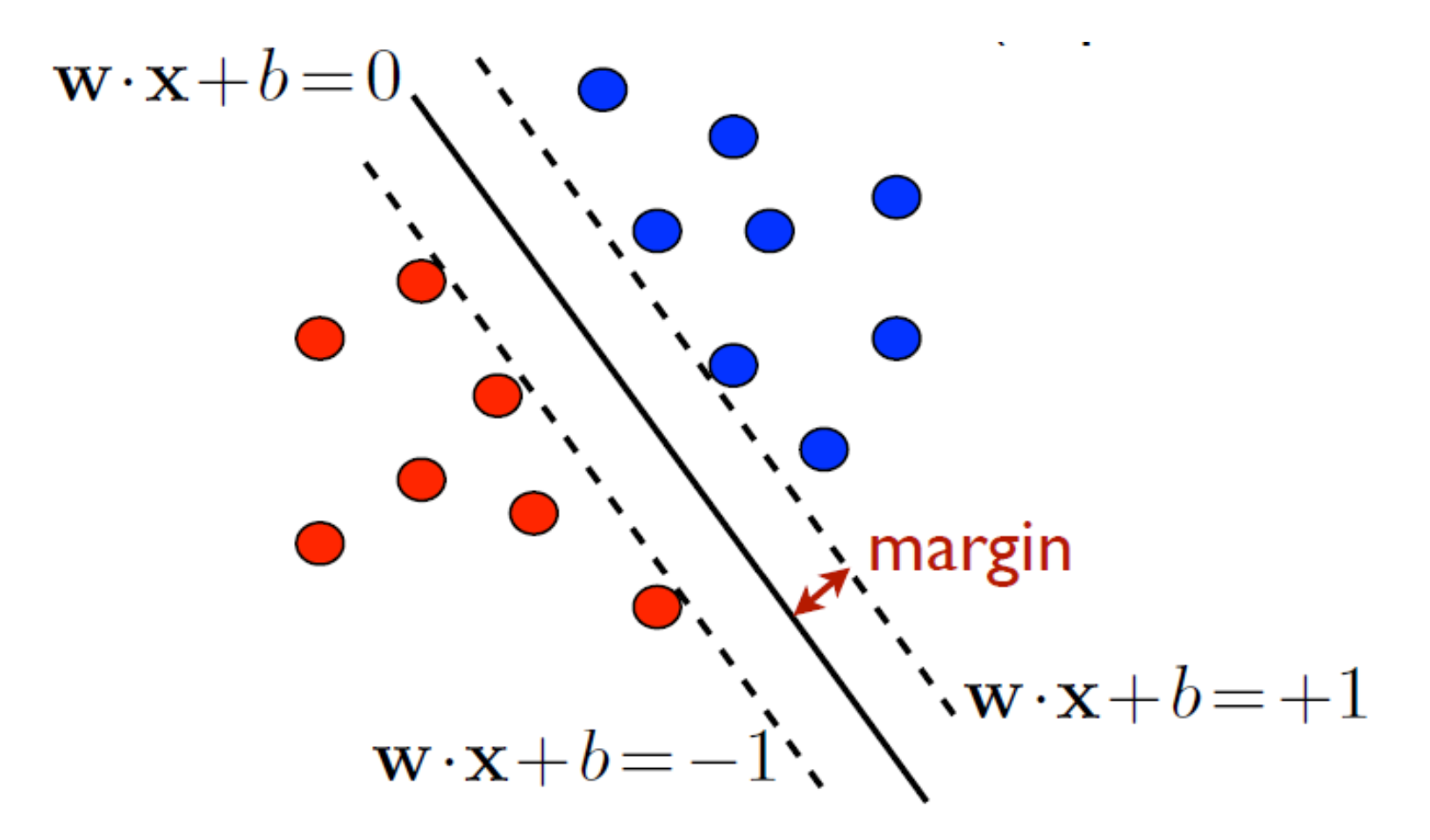
위에서 언급한 것과 같이 positive는 +1, negative -1로 계산한다. 이렇게 하면 실선인 classifier은 margin에 해당하는 점선들 사이에 위치하게 된다.

+2, +3 이렇게 하지 않는 이유는 어차피 상수항이기 때문이다.

우리는 $x$와 $y$가 주어졌을 때 $w$와 $b$를 찾자.

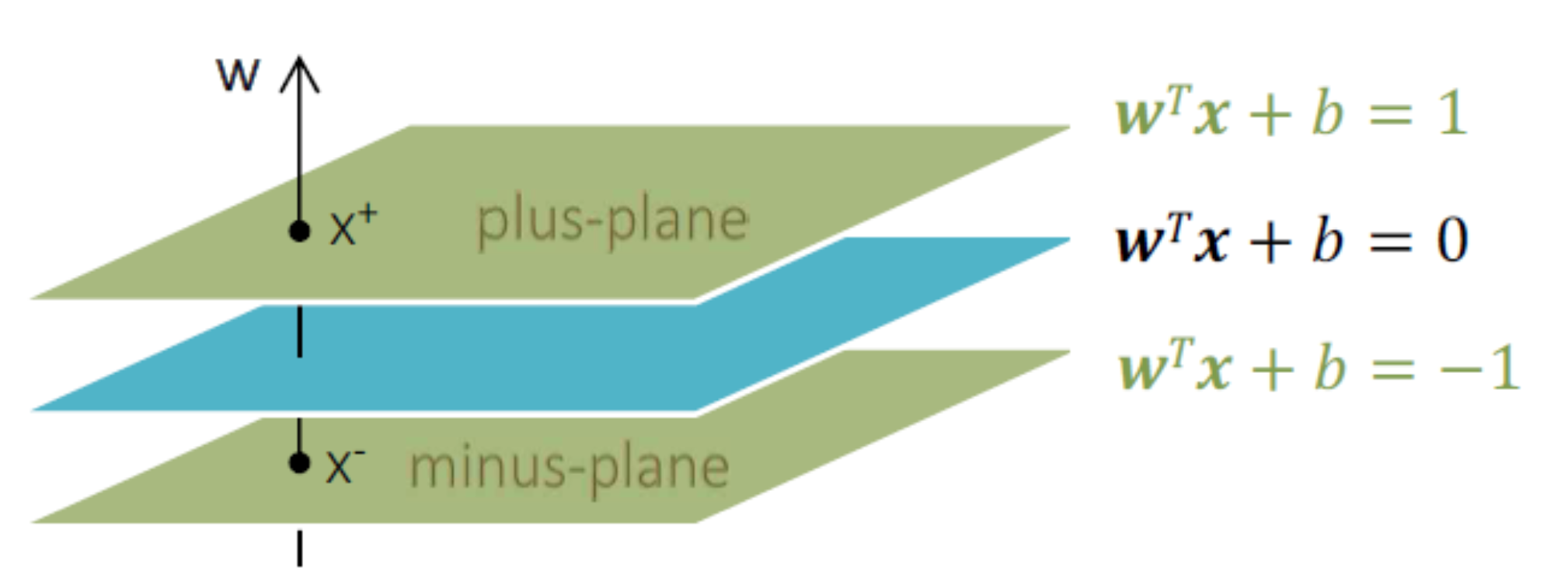
우선은 margin의 넓이를 구해보자. 3차원 space라고 했을 때, 청록색이 분류면, 초록색이 margin이라고 했을 때, 분류면 기준으로 위아래를 마진으로 측정하거나, 이것의 $\frac{1}{2}$을 한다. 우리는 $\frac{1}{2}$을 기준으로 margin을 측정하자.

$x_{0}$가 분류 경계면에 있다고 하자. $w^{T}x_{0}+b=0$이고, $x_{1}$을 위쪽 마진에 있는 값이라고 하자. $x_{1}=x_{0}+pw$라고 표현할 수 있다. 그러면 $w^{T}(x_{0}+pw)+b=1$로 되고, 이를 다시 쓰면 $wx_{0}+pw^{T}w+b=1$로 표현이 가능하다. $pw^{T}w=1$이니깐 $p=-\frac{1}{w^{T}w}$가 된다. 여기서 음수를 제거하면 아래와 같은 margin 식을 구할 수 있다.

$$ margin = \frac{1}{\parallel \mathbf{w} \parallel^{2} } $$

왜 margin을 늘리는 게 capacity를 줄일까? 아래식을 살펴보자.

$$ h \leq min(\lceil \frac{R^{2}}{\Delta^{2}} \rceil, D)+1 $$

VC-dimension 자체는 margin $\Delta$에 bound 된다. 위 식에서 $D$는 차원의 수, $R$은 범주와 상관없이 전체 데이터를 입력 공간에서 감싸는 hyper sphere의 반지름이다.

위 식에서 우리가 컨트롤할 수 없는 것은 $R$이고, 가변적인 것은 margin을 어떻게 설정하냐에 따라 달라진다.

식을 보면 $\Delta$가 커지면 분수 식은 작아진다. 이게 충분히 작아지면 차원 $D$보다 작아지는 경우가 발생하게 된다. 그러면 VC-dimension 자체가 $D+1$보다 작아질 수 있다.

따라서 margin을 최대화하는 것은 VC-dimension을 줄이는 효과를 가지고, 이는 아래 식에서 $h$를 줄인다. 따라서 전체 수식의 capacity term은 작아진다.

$$ R[f] \leq R_{emp}[f]+\sqrt{\frac{h(\ln{\frac{2n}{h}}+1)-\ln{\frac{\delta}{4}}}{n}} $$

결국은 함수의 risk를 줄이기 위해서 train error가 동등하면 margin이 최대화되는 점을 찾으면 된다.

SVM은 아래와 같이 4가지 케이스로 나뉜다.

위 표에서 Hard margin은 마진을 벗어나는 예외를 허용하지 않는 것이고, Soft margin은 예외를 허용하는 것이다. 예외 허용은 penalty term을 도입한 것이다.

선형 분류가 가능한지 불가능한지에 따라 위와 같이 나눈다.

Case 1에 해당하는 선형 분류가 가능하고, Hard margin을 사용하는 경우를 보자.

SVM case 1: Linear Case & Hard Margin

해당 케이스의 objective function은 다음과 같이 정의된다.

$$ \text{Objective function}=\min{\frac{1}{2}\parallel \mathbf{w} \parallel^{2}} $$

우리가 알고 있는 margin에 대한 식은 $\frac{1}{\parallel \mathbf{w} \parallel^{2} }$이고, 이를 튜닝을 해야 하는데, 이에 대해 역수를 취하면 최소화 문제로 만들 수 있다. 이를 보면 $y$를 왜 $+1,-1$로 했는지 이해가 될 것이다.

아래 그림을 보자.

위 그림에서는 $x, y$ㄷ가 주어지고, 이를 통해 우리가 찾아야 하는 parameter는 $\mathbf{w}$와 $b$이다. 이를 바탕으로 보면 실선은 $\mathbf{w}\cdot \mathbf{x}+b$인 classifier이고, 여기서 margin을 $+1, -1$로 잡으면 모든 파란색 $\mathbf{x}$는 $+1$보다 위 쪽에 위치하게 되고, 빨간색은 $-1$보다 더 작아햐 한다.

이를 식으로 살펴보면, 만약 $y_{i}=+1$ 이면 $\mathbf{w}\cdot \mathbf{x} \geq 1$이여야 하고, 빨간색은 반대인 $\mathbf{w}\cdot \mathbf{x} \leq -1$가 되어야 한다.

이를 양변에 $y_{i}$를 곱하면 파란색의 경우 부등호가 그대로지만, 빨간색은 부등호가 반대로 된다.

이렇게 되면 모든 $i$에 대해 식이 아래 식과 같아진다.

$$ y_{i}(\mathbf{w}^{T}x_{i}+b)\geq 1 $$

우리는 이 식을 라그랑주 승수 법을 통해 최적화 식으로 변형해야 한다.

라그랑주 승수법 복습

라그랑주 승수 법에 대해 remind 해보자.

예를 들어 $\min{\frac{1}{2}x^{2}-2x+3}$라는 식이 존재하고, $x \geq 2$라는 조건이 있을 때, 우리는 제약식을 없애기 위해 라그랑주 승수법을 이용한다. 결과는 다음과 같다.

$$ L_{p}=\frac{1}{2}x^{2}-2x+3-\lambda(x-2) $$

여기서 $x-2$는 $x-2\geq 0$이라는 조건에서 나온 것이다.

위 라그랑주 식에서 극소점을 찾으려면 $x$에 대해 편미분을 진행하면 된다. 결과는 다음과 같다.

$$ x-2-\lambda=0 $$

식을 정리하면 $x=2+\lambda$로 쓸 수 있고, 우리는 $x$를 $L_{p}$에 넣을 수 있다. 이를 wolfe’s dual problem이라고 한다.

식을 정리하면 다음과 같이 쓸 수 있다.

$$ L_{D}:-\frac{1}{2}\lambda^{2}+1,\ \lambda \geq 0 $$

위 식은 dual problem이기 때문에 $L_{D}$에 대한 $max$ 문제가 된다.

$L_{p}$ 식의 $\lambda$ 부분의 의미는 $(2,1)$을 지나는 곡선에서 $x$가 2보다 큰 부분을 사용할 수 있다는 것이다.

$x=2$일 때 $f(x)=1$이라는 것을 알 수 있다. 이것이 $L_{p}$에 대한 문제이고, $L_{D}$의 문제에서는 $(0,1)$을 지나는 음수 곡선에서 $\lambda=0$일 때, $L_{D}=1$이 된다. 이렇게 되면 $L_{p}$의 최솟값과 $L_{D}$의 최댓값이 같아진다.

이렇게 보면 두 방법 모두 쉽지만 $L_{D}$로 풀면 훨씬 쉬워진다.

$$ y_{i}(\mathbf{w}^{T}x_{i}+b)\geq 1 $$

다시 우리의 식으로 돌아와서 우리의 objective function에 라그랑주 승수법을 적용하면 다음과 같이 계산이 된다.

$$ \min{L_{p}}(\mathbf{w}, b, \alpha_{i})=\frac{1}{2}\parallel\mathbf{w}\parallel^{2}-\sum_{i=1}^{N} \alpha_{i}(y_{i}(\mathbf{w}^{T}\mathbf{x}_{i}+b)-1) \\ s.t. \ \ \alpha_{i} \geq 0 $$

KKT condition을 적용해서 $\mathbf{w}$와 $b$가 미지수이기 때문에 편미분을 취하면 아래와 같은 식이 된다.

$$ \frac{\partial L_{p}}{\partial \mathbf{w}}=0 \rightarrow \mathbf{w}=\sum_{i=1}^{N}\alpha_{i}y_{i}\mathbf{x}_{i} $$

$$ \frac{\partial L_{p}}{\partial b}=0 \rightarrow \sum_{i=1}^{N}\alpha_{i}y_{i}=0 $$

이 수식을 가지고 원래의 $L_{p}$ 식에 적용하면 다음과 같이 정리된다.

$$ \max L_{D}(\alpha_{i})=\sum_{i=1}^{N}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}\mathbf{x}^{T}_{i}\mathbf{x}_{j} \\ s.t. \ \sum^{N}_{i=1}\alpha_{i}y_{i} = 0\ and \ a_{i} \geq 0 $$

Primal 문제가 Dual 문제로 바뀐다.

우리는 새로운 입력 데이터 $x_{new}$를 도입하면 다음과 같이 식이 전개된다.

$$ f(\mathbf{x}_{new})=sign(\sum^{N}_{i=1}\alpha_{i}y_{i}\mathbf{x}_{i}^{T}\mathbf{x}_{new}+b) $$

binary classification을 해야 되기 때문에 sigmoid function을 적용하였다.

$$ \alpha_{i}(y_{i}(\mathbf{w}^{T}\mathbf{x}_{i}+b)-1)=0 $$

만약 위 식이 0이 되었을 때, KKT condition에 의해 $\alpha$ 또는 $y_{i}(\mathbf{w}^{T}\mathbf{x}_{i}+b)-1$ 둘 다 0이 되면 안된다. 둘 중 하나만 0이 되어야 한다.

이 의미는 만약 term 2가 0이라는 것은 margin 경계선 위에 걸쳐 있는 데이터라는 의미이고, $\alpha$는 supprot vector라고 부른다. support vector는 0이 되면 안된다.

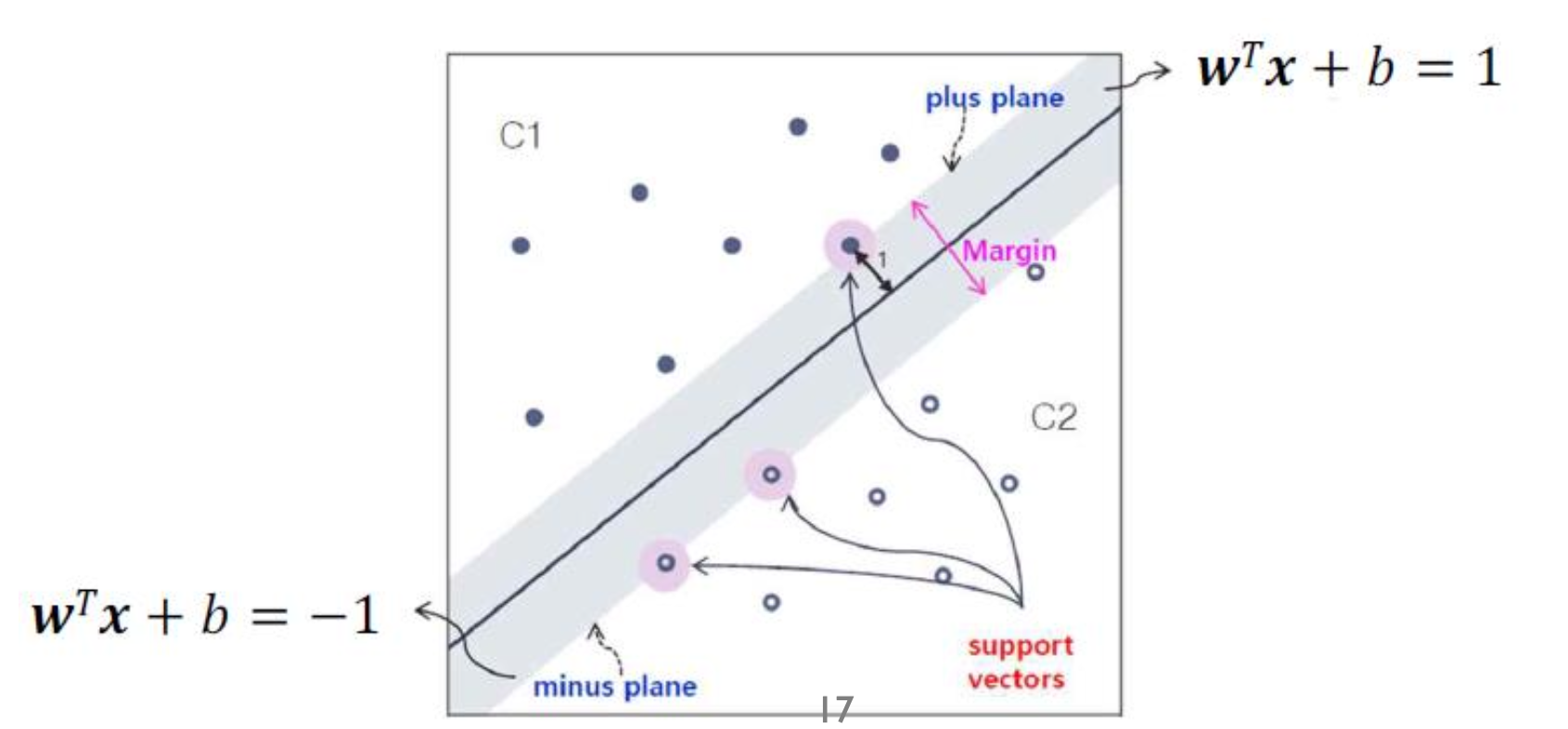
위 그림에서 margin에 걸쳐 있는 3개의 점이 바로 support vector이고, $\mathbf{w}$를 결정하는데 영향을 미친다. 이는 굉장히 중요한 개념이다.

$b$는 미지수인데, 별로 고려하지 않는 이유는 어떤 특정한 support vector에 대해서는 $\mathbf{w}$ 대신 summation 식을 넣으면 구할 수 있다. 원래 $b$는 각 위치에 따라 같아야 하지만, 위치마다 살짝 다르다. 보통 $b$는 각 $b$의 평균값을 사용한다고 한다.

우리는 SVM을 풀었을 때 margin의 size를 직접 계산할 수 있다.

support vector는 margin 위에 존재하는 점이기 때문에 $\mathbf{w}^{T}\mathbf{x}+b=y_{i}$가 성립한다. 이를 바탕으로 전개를 하면 $b$에 대한 식으로 나타낼 수 있다.

$$ b=y_{i}-\sum_{i=1}^{N}\alpha_{i}y_{i}(\mathbf{x}{j}, \mathbf{x}{i}) $$

그리고 이 식에 $\sum_{i=1}^{N}\alpha_{i}y_{i}$를 곱하면 다음과 같이 식이 전개된다.

$$ \sum_{i=1}^{N}\alpha_{i}y_{i}b=\sum_{i=1}^{N}\alpha_{i}y_{i}^{2}-\sum_{i,j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}(\mathbf{x}{i}, \mathbf{x}{j}) $$

위 식에서 $b$는 상수니깐 나가고, $\alpha y$는 0이 된다. $y^{2}$는 1이 된다. 따라서 아래와 같이 된다.

$$ 0=\sum_{i=1}^{N}\alpha_{i}-\mathbf{w}^{T}\mathbf{w} $$

우리가 위에서 구한 margin 식에 위 식을 대입하면 최종적인 margin의 크기를 구할 수 있다.

$$ \rho^{2}=\frac{1}{\parallel \mathbf{w} \parallel^{2}_{2}}=\frac{1}{\sum_{i=1}^{N}\alpha_{i}}=\frac{1}{\parallel \mathbf{\alpha} \parallel_{1} } $$