Machine learning: Linear Regression (MLE)

Linear regression은 supervised learning에서 많이 사용되고, 앞에서 살펴보았던 kernel이나 basis expansion 등을 이용해 Non-linear relationship을 가진 model을 만들 수 있었다.

우리는 아래 수식과 같이 parameter들을 주로 Gaussian을 사용하여 modeling을 진행했었다.

$$ \text{Linear regression model:}\ \ p(y\mid {x}, {\theta}) = \mathcal{N}(y\mid w^{T}x, \sigma^{2}) $$

$$ \text{Non-linear regression model:}\ \ p(y\mid {x}, {\theta}) = \mathcal{N}(y\mid w^{T}x\phi(x), \sigma^{2}) $$

$$\phi(x) = [1,x,x^{2}, \dots, x^{d}] $$

Basis expansion을 사용한다고 할 때 input feature vector인 $x$를 weight인 $w$와 바로 곱하지 않고, basis function인 $\phi(x)$와 곱해준다. basis function은 위 수식과 같이 표현할 수 있다.

한 가지 생각을 보면 linear regression을 Gaussian을 이용해 modeling 할 수 있었던 이유는 무엇일까?

이는 residual error를 Gaussian을 통해 assumption 할 수 있기 때문이다.

그리고 Non-linear regreesion modeling을 진행해도 basis function을 이용한 결과는 여전히 linear regression에 대한 문제이다. 그 이유는 $w$와 $\phi(x)$의 관계가 여전히 선형 관계이기 때문이다.

 

Maximum Likelihood Estimation (least squares)

본격적으로 우리는 결과적으로 최적화된 parameter를 찾는 방법에 대해 논할 것이다. parameter를 찾는 방법은 여러 가지 많지만 MLE (Maximum Likelihood Estimation)를 중심으로 먼저 살펴보자.

MLE 수식을 계산하기 위해 weight를 추정하는 통계적 수식은 다음과 같이 정의할 수 있다.

$$ \hat{\theta} = argmax_{\theta}{\log{p(\mathcal{D} \mid \theta)}} $$

식을 간략하게 설명하면 train data와 weight 간 최적화하는 지점을 찾는다. 이는 로그를 써서 최대화할 수 있는 $\theta$인 weight 값을 찾는다.

위 수식에서 $\mathcal{D}$는 train dataset을 의미하고, 이는 $\mathcal{D} = \left\{ x_{1}, \dots, x_{n} \right\}$로 정의된다. $\mathcal{D}$ 가 $\text{i.i.d.}$를 만족한다면 우리는 Log-likelihood의 식을 정의할 수 있다.

$$ \mathcal{l}= \log{p(\mathcal{D} \mid \theta)} = \sum_{i = 1}^{N}{\log{(y_{i} \mid x_{i}, \theta})} $$

위 식은 weigth 추정 수식의 $\log p()$와 같다. 이는 Log likeli-hood라고 부른다.

우리는 Log likeli-hood를 최대화하는 것과 NLL (Negative log likeli-hood)를 최소화하는 것이 같다는 것을 알 수 있다. (log 함수의 특성)

NLL의 수식은 다음과 같다.

$$ \text{NLL}(\theta) = -\sum_{i = 1}^{N}{\log{(y_{i} \mid x_{i}, \theta})} $$

NLL은 Log likeli-hood에 -를 붙인 것과 같다.

Maximum 하는 문제보다는 Minimum 하는 문제가 software optimization 측면에서는 때때로 더 편리하다.

이제 위에서 구한 수식을 활용하여 MLE의 적용을 해보자. Log likeli-hood에 Gaussian를 적용하면 다음과 같다.

$$ \mathcal{l}(\theta) = \sum_{i=1}^{N}{\log{\left[\left(\frac{1}{2\pi \sigma^{2}}\right)^{\frac{1}{2}}\text{exp}{\left(-\frac{1}{2\sigma^{2}}\left(y_{i}- w^{T}x_{i}\right)\right)^{2}}\right]}} \\ = -\frac{1}{2}\text{RSS}(w) - \frac{N}{2}\log(2\pi \sigma^{2}) $$

$\text{RSS}$는 residial sum of square의 약자이고 다음과 같이 정의된다.

$$ \text{RSS}(w) = \sum_{i =1}^{N}(y_{i} - w^{T}x_{i})^{2} $$

$\sum$ 안에 존재하는 식들이 residual error이다. 이는 정답 label $y$ 에 대한 input vector $x$ 와 weight인 $w$에 대한 차의 제곱이다. 우리는 optimization을 위해 residual error를 최소화해야 하는데, 이들의 합에 대해 최소화를 진행한다. $\text{RSS}$는 $\text{SSE}$(sum of squared error)라고도 불리는데, 이를 data size인 $N$ 만큼 나누게 된다면 $MSE$ 수식이 된다.

$$ MSE = \frac{SSE}{N} $$

결과론적으로 우리는 $\text{RSS}$ 에 대해 $l_{2} \ norm$을 적용할 수 있다. 식은 다음과 같다.

$$ RSS(w) = \Vert \epsilon \Vert_{2}^{2} = \sum_{i=1}^{N}\epsilon^{2}{i}, \ \text{where} \ \epsilon{i} = (y_{i} - w^{T}x_{i}) $$

우리는 이제 $RSS$를 최소화하여 $w$에 대한 $MLE$ 수식을 구해야 한다. 이 문제를 least squares라고 부른다.

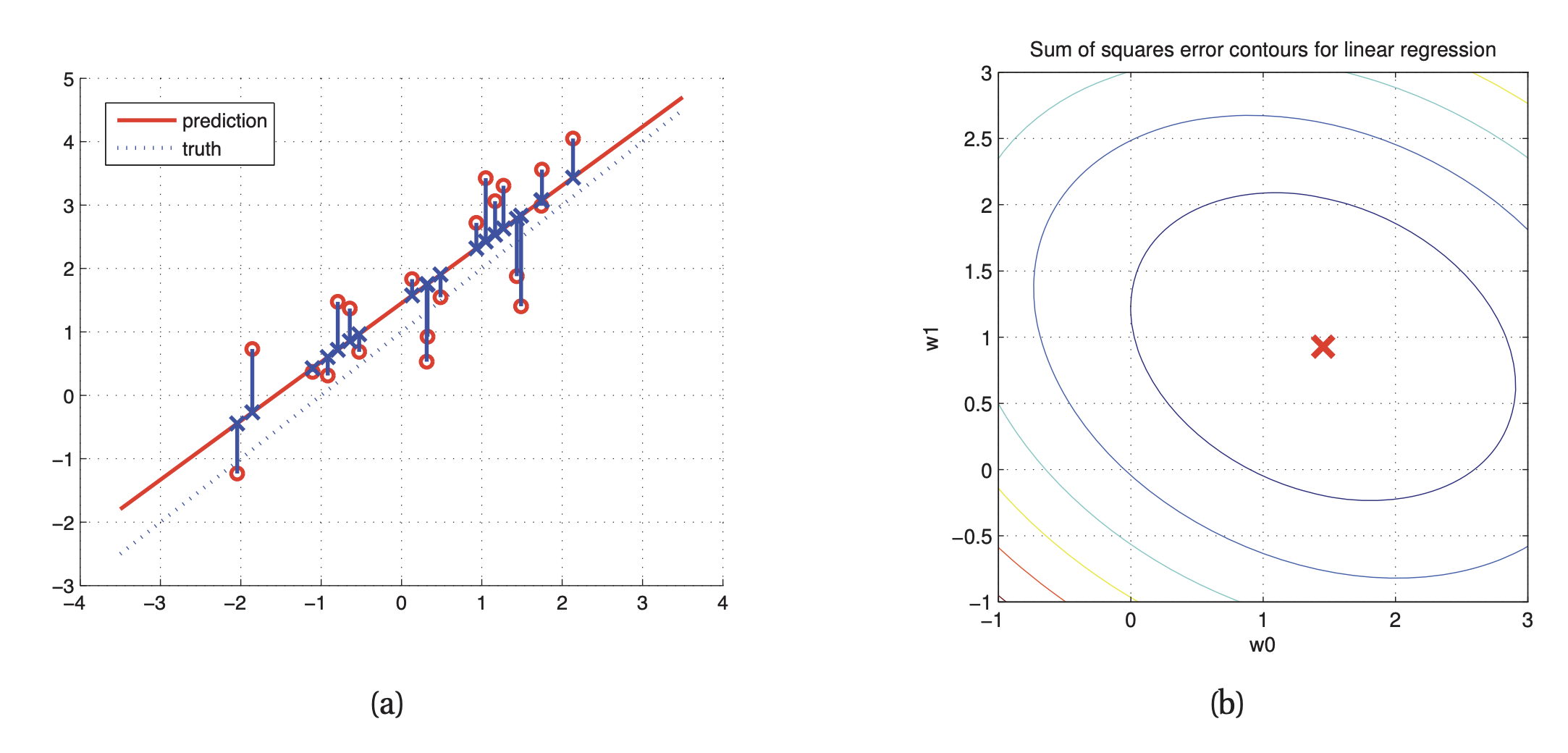
(a)는 linear least squares에서 training point (빨간 원)으로부터 distance의 합들이 최소화되는 지점 (파란색 point 부분)을 찾아 regression line을 표현한 그림이다. regression line을 통해 error를 최소화할 수 있다.

(b)는 $RSS$의 등고선으로 표현한 모습이다. 빨간색 부분이 최적의 $w_{0}, w_{1}$ 지점에서의 $MLE$ 를 표현한다. (등고선으로 표현한 이유는 basis function expansion을 사용해 Non-linear 하게 표현한 예시이기 때문이다.)

이제 본격적으로 $MLE$에 대한 수식을 설계해보고 optimization을 통해 최적의 $w$를 구해보자.

우선 $w$에 대한 objection function이 필요하다. 수식을 다음과 같이 정의할 수 있다.

위에서 정의한 $RSS(w)$를 활용하자.

$$ RSS(w) = \Vert \epsilon \Vert_{2}^{2} = \Vert y-Xw \Vert^{2} = (y-Xw)^{T}(y-Xw) \\ =y^{T}y - y^{T}Xw - w^{T}X^{T}y - w^{T}X^{T}Xw $$

위 수식은 $RSS$에 대한 $l_{2} \ norm$을 적용하여 풀어서 쓴 수식이다.

우리는 결국 전체적으로 보면 $argmin_{w}$를 찾는 문제인데, 이는 $RSS$의 gradient가 0이 될 때의 $w$ 값을 찾으면 된다.

Gradient를 적용하기 전, 아래의 미분 공식을 알면 계산하기 편하다.

$$ \frac{\partial(b^Ta)}{\partial a} = b, \ \frac{\partial(a^{T}Aa)}{\partial{a}} = (A+A^{T})a $$

이제 본격적으로 $RSS$에 대해 미분을 해보자.

$$ \frac{\partial RSS(w)}{\partial w} = \frac{\partial}{\partial w}(y^{T}y - y^{T}Xw - w^{T}X^{T}y - w^{T}X^{T}Xw) \\ = -2X^{T}y + 2X^{T}Xw \rightarrow 2X^{T}y = 2X^{T}Xw \\ \therefore \hat{w} = (X^{T}X)^{-1}X^{T}y $$

$\hat{w}$로 쓴 이유는 estimation value 이기 때문이다.

이로써 최종적으로 구해야 하는 $w$를 정의하였다. 이를 OLS (ordinary least squares)라고 부른다.

이번엔 least square 문제에 대해 기하학적 해석의 관점으로 보자.

$N > D$라고 가정하자. 쉽게 말하자면 $N$은 데이터의 카테고리, $D$는 데이터의 크기이다.

우리가 사용할 variable의 정의는 다음과 같다.

$$ \tilde{x}{j} \in \mathbb{R}^{n}:\text{ j'th column of} \ X \\ x{j} \in \mathbb{R}^{D}:\text{ i'th data case of} \ X \\ y \in \mathbb{R}^{N}: \text{a target values} $$

우리의 문제는 결국에는$y$와 최대한 가까운 linear subspace에 $\hat{y} \in \mathbb{R}^{N}$를 만족하는 벡터를 찾는 것이다.

이를 수식으로 표현하면 다음과 같다.

$$ argmin_{\hat{y}\in span(\left\{ \tilde{x}{1}, \dots, \tilde{x}{D} \right\})} \Vert y-\hat{y} \Vert_{2} $$

$y$와 $\hat{y}$의 $l_{2} \ norm$을 한 최솟값을 만족시키는 공간을 찾으면 되는 것이다.

$\hat{y}$는 어떠한 span이기 때문에 $w$와 $X$의 선형 결합으로 표현할 수 있다.

$$ \hat{y} = w_{1}\tilde{x}{1}+ \dots +w{D}\tilde{x}_{D} = Xw $$

이제는 residual error를 줄이는 방법에 대한 수식을 정의해야 한다. 이를 위해 우리는 $X$의 모든 column에 대해 직교하는 residual vector를 찾아야 한다. 따라서 아래와 같이 수식을 정의할 수 있다.

$$ \tilde{x}^{T}_{j} (y - \hat{y}) = 0 \ \text{for} \ 1:D \\ \rightarrow X^{T}(y - Xw)=0 \\ \rightarrow \hat{w} = (X^{T}X)^{-1}X^{T}y $$

결국 $RSS$의 미분과 같은 식을 얻게 된 것을 확인할 수 있다.

또한 $\hat{y}$ 에 위 식을 적용하면 다음과 같다.

$$ \hat{y} = X\hat{w} = X(X^{T}X)^{-1}X^{T}y $$

$y$를 column space $X$에 orthogonal projection 한다고 할 수 있다.

여기서 projection matrix는 아래 수식과 같고, 이는 hat matrix라고도 불린다.

$$ P = X(X^{T}X)^{-1}X^{T} $$

$$ \text{span}(s)= \left\{ \sum_{k=1}^{K}\lambda_iv_i\mid{v_i\in S} \right\} $$

이거 추가하기, orthogonal을 찾는 이유는 distance가 가장 짧기 때문이다.

 

Convexity

convexity는 optimization과 연관이 있다. convexity를 통해 최적화된 $argmin{f(\theta)}$를 찾는다. 어떤 function이 optimization에 수월하게 되려면 convexity가 높아야 한다. convext의 정의는 다음과 같다.

$$ \lambda \theta + (1 - \lambda)\theta' \in S, \forall \lambda \in [0,1] $$

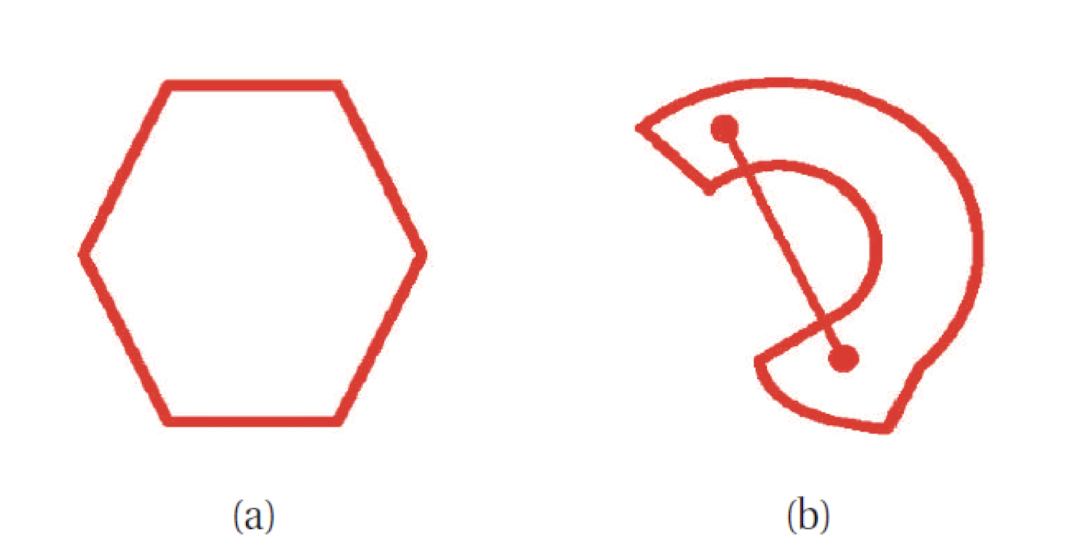
위 그림을 보면서 설명을 하자면 어떠한 space $S$ 안에 임의의 2개 점을 선정하면 $\theta$와 $\theta'$이라고 둘 수 있다. point 사이의 line을 두는데 이 line을 $\lambda \theta + (1 - \lambda)\theta'$ 라고 표현할 수 있다. line을 표현하는 point들이 $S$ 안에 있어야 한다. 이를 통해 해당 space가 convex 한지 알 수 있다. 그림 (b)는 $S$ 에 속하지 않은 점들이 있어서 convext가 아니다.

위 정의를 이용해서 convex function을 정의하면 다음과 같다.

$$ f(\lambda\theta+(1-\lambda)\theta') \leq \lambda f(\theta) + (1-\lambda)f(\theta') $$

수식의 의미는 그래프 위 임의의 2 점을 \theta, \theta'라고 할 때, 해당 점을 기준으로 그린 line보다 f(x)가 더 아래 있으면 f(x)를 convex function이라고 한다.

해당 그래프는 Non convex function이다.

Convex function의 정의에 의해 global optimization을 구할 수 있다. 이는 $f(\theta)$를 최소화하면 된다.

위 그림에서는 조금 다르다. 시작 지점에 따라 global optimization을 찾을 수도 있고 못 찾을 수도 있다. 따라서 적당한 지점의 $\theta$를 설정해야 한다.

convex의 반대는 concave이다. 이는 convex function $f(x)$에 음수를 취하면 된다.

concave function = $-f(x)$ $(f(x) \text{ is convex function})$

각 함수 $\theta^{2}, \log{\theta}, e^{\theta}, \theta\log{\theta}, \sqrt{\theta}$ 들을 convex인지 concave인지 구분해보자.

$\text{convex: }\theta^{2},e^{\theta}, \theta\log{\theta}$

$\text{concave: }\theta\log{\theta}, \sqrt{\theta}$

Convex function은 반드시 unique global minumum $\theta^{*}$를 갖는다.

또한 2번 미분한 값이 반드시 양수여야 한다.

$$\frac{d^{2}}{d\theta^{2}}f(\theta) > 0 $$

만약 $f(\theta)$ 가 스칼라 함수가 아니라 multivariate function이면 2번 미분해서 양수면 convex이다.

Hessian metrix를 적용하면 다음과 같다.

$$ H_{ik} = \frac{\partial f^{2}(\theta)}{\partial x_{i}x_{k}} $$

참고로 Hessian metrix는 다음과 같다.

$$ H_{f} = \begin{pmatrix} \frac{\partial^{2} f}{\partial x_{1}^{2}} \cdots \frac{\partial^{2} f}{\partial x_{1} \partial x_{m}} \\ \ddots \\ \frac{\partial^{2} f}{\partial x_{n} x_{1}} \cdots \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{pmatrix} $$

 

Robust Linear Regression

Linear regression의 한계는 outlier에 대해 민감하다. 따라서 이에 대해 결과에 영향을 줄 수 있다.

$$ \text{RSS}(w) = \Vert y - \bar{y} \Vert_{2}^{2} $$

그 이유는 위 수식과 같이 regression을 할 때 이와 같이 error를 측정하면서 $y$에 대한 값이 outlier이면 norm이라 매우 민감하다. 따라서 이를 해결하기 위해 해결책이 필요하다. 우리는 지금까지 $p$에 대해 Gaussian 분포로 가정했다.

기존 Gaussian distribution에서 heavy tail을 같은 distributio이 필요하다. 즉 Gaussian distribution은 양 끝으로 갈수록 tail에 대해 민감해지는데, 이를 다른 분포를 통해 해결할 수 있다.

Laplace distribution은 log lilehood가 더 작기 때문에 outlier에 대해 덜 민감하다.

Laplace distribution의 정의는 다음과 같다.

$$ \text{Lap}(x \mid \mu, b) \propto \frac{1}{2b}\text{exp}(- \frac{\mid x - \mu\mid}{b}) $$

그리고 이에 대해 likelihood를 maximum 하는 $\theta$에 대한 수식은 다음과 같다.

$$ argmax_{\theta}\log{p(\mathcal{D}\mid \theta)} \propto -\frac{\mid x - \mu \mid}{b} $$

하지만 위 수식은 절댓값이 존재하는 함수이기 때문에 선형적이지 않다. Non-linear function은 미분이 불가능해 global optimal을 찾기 힘들다. 하지만 convex function에 속한다.

Huber loss function

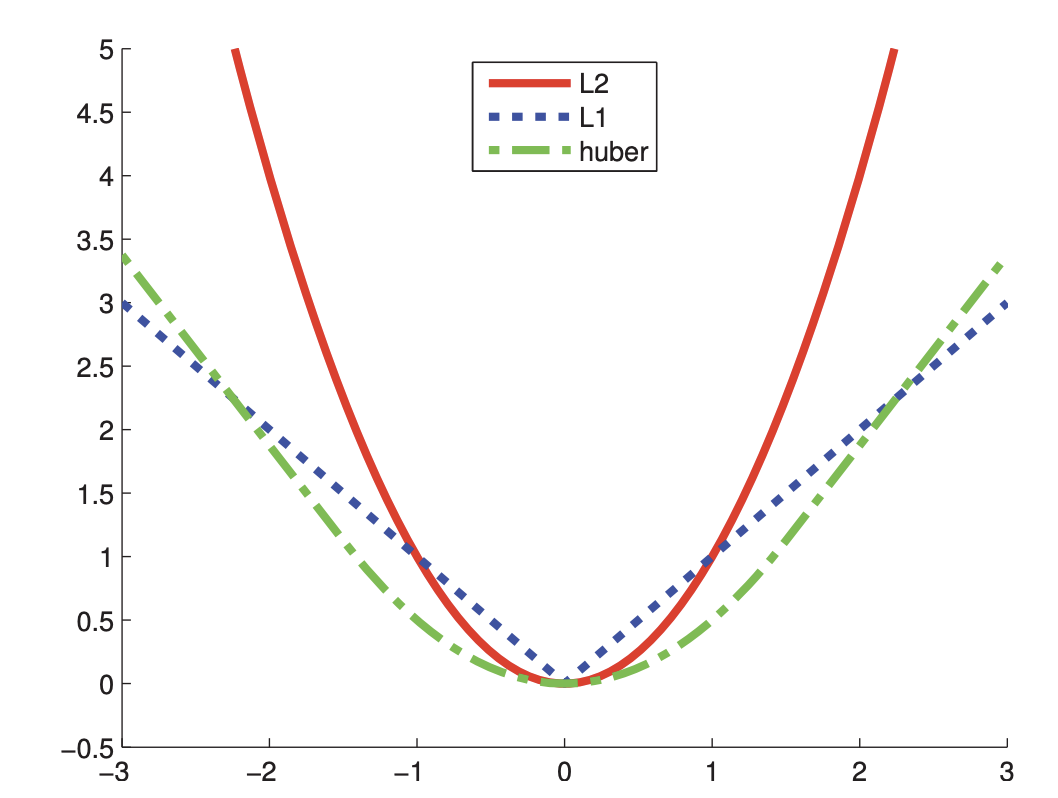
Laplace를 보완하기 위해 Huber loss function이 등장했다. 다음과 같이 정의된다.

$$ L_{H}(r, \delta) = \begin{cases} \frac{r^{2}}{2} \ \ \ \ \text{if} \mid r\mid \leq \delta \\ \delta \mid r \mid - \frac{\delta^{2}}{2} \ \ \ \ \text{if} \mid r\mid > \delta \end{cases} $$

$\mid r \mid < \delta$ 일 때는 $l_{2}$ 에 대한 error로 사용하고, $\mid r\mid > \delta$ 일 때는 $l_{1}$ 에 대한 error로 사용하면 된다.

이를 통해 Laplace에 비해 optimal을 빠르게 찾을 수 있다.

Ridge Regression

Overfitting 이란 model이 train data를 더 잘 표현하기 위해 더 복잡해지는 경우를 의미한다. train error는 작지만 test error가 큰 경우를 말한다. 만약 train data에 noise가 있으면 noise에 대한 학습까지 진행한다. 만약 non-linearity로 한다고 가정할 때 다음과 같다.

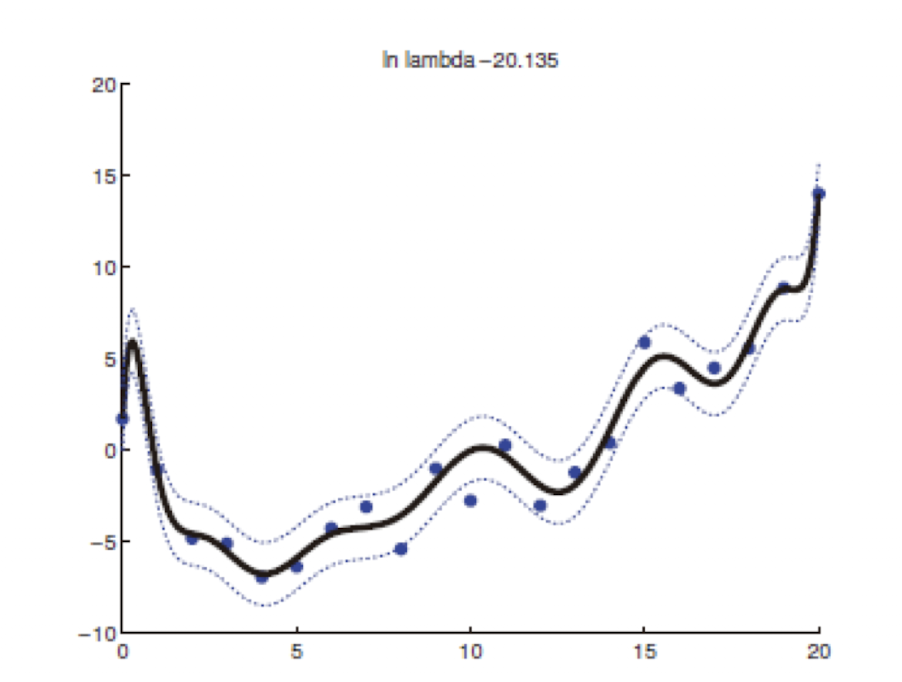
위 그림에서는 dimension이 14인 경우이다. 그래프가 매우 복잡 해지고, cost를 계산하면 단순한 linear model보다 훨씬 복잡해진다.

overfitting이 생기는 이유를 least square 관점에서 볼 때 $w$ 에 해당하는 coeefficient 값들은 다음과 같이 나오게 된다.

이 값들을 보면 매우 크거나 매우 작은 값들이 많다. overfitting의 경우에는 이렇게 $w$ 가 들쑥날쑥 하다.

이렇게 된다면 위 그래프와 같이 커브가 왔다 갔다 한다. 또한 data가 약간 변화하면 이에 대해 매우 민감하게 바뀐다. 이 문제를 완화하려면 어떻게 해야 할까?

이는 바로 $w$ 값을 작게 만들면 된다. 이로 인해 보다 부드러운 curve를 만들 수 있다. 따라서 $w$ 에 대해 prior를 직영 시킨다. 그리고 조금 더 simple하게 설계하기 위해 Zero-mean Gaussian을 사용한다.

$$ p(w) =\prod_j{\mathcal{N}(w_{j} \mid 0, \tau^{2})} \\ \frac{1}{\tau^{2}} \text{ :controls the strength of the prior}
$$

Zero-mean Gaussian이기 때문에 $w$의 값이 커지면 0에 가까워진다.

MAP는 lilkelihood와 prior를 가지고 정의가 된다. 식은 다음과 같다.

$$ \begin{align} argmax_{w}\sum_{i=1}^N\log\mathcal{N}(y_i|w_0+{w}^T{x}i,\sigma^2)+\sum{j=1}^D\log\mathcal{N}(w_j|0,\tau^2) \end{align} $$

이를 재구성하면 다음과 같다.

$$ J(w) = \frac{1}{N} \sum_{i=1}^{N}(y_{i} - (w_{0} + w^{T}x_{i}))^{2} + \lambda \Vert w \Vert^{2}_{2} $$

여기에서, $\lambda\triangleq\sigma^2/\tau^2\ge0$ 이고, $\Vert{w}\Vert_2^2=\sum_jw_j^2={w}^T{w}$ 이다. 또한 First term 은 $\text{MSE}/\text{NLL}$ 을 의미하고, Second term 은 complexity penalty를 의미한다.

이제는 이렇게 구한 $J(w)$에 대해 다음과 같이 최적화할 수 있다.

$$ argmax_{w}{\frac{\partial J(w)}{ \partial w}} \Leftrightarrow \hat{w}_{ridge} = (\lambda I_{D} + X^{T}X)^{-1}X^{T}y$$

$\hat{w}{ridge}$를 살펴보면, 앞서 구했던 $\hat{w}{OLS}$에 complexity penalty 인 $\lambda I_{D}$가 추가된 것을 확인할 수 있다.

이러한 technique을 ridge regression 또는 penalized least squaures라고 한다.

일반적으로 Gaussian prior를 model의 parameter에 추가하여 이를 작게 만드는 것을 $l_{2}$ regularization 또는 weight decay라고 부른다. 알아두어야 할 것은 offset term (혹은 bias term)인 $w_{0}$ 은 함수의 높이에만 영향을 미치고 model complexity에는 영향을 주지 않기 때문에 regularization 하지 않는다.

weight 크기의 합에 panelty를 줌으로써, function이 simple함을 보장할 수 있다. ($w = 0$ 은 simplest function인 straight line에 해당하고, constant에 해당하기 때문이다.)

정리하자면, prior를 추가하는 것을 통해 MAP를 수행할 수 있고, 이를 reformulation 한 $J(w)$를 통해 $\hat{w}_{ridge}$를 구하게 되면 model이 data에 잘 fitting 하면서 overfitting도 줄일 수 있는 linear curve line을 만들 수 있다.