Machine learning: Logistic Regression (MLE ~ Multi-class Logistic Regression)

Introduction

Probabilistic classifier의 목적은 어떠한 label에 대해 확률 적으로 추론하는 것이다.

Generative approach는 $p(y,x)$의 joint model을 찾은 후, vector $x$의 조건에 따라 $p(y \mid x)$를 구했다.

Discriminative approach는 $p(y \mid x)$를 바로 구하기 위해 model을 fitting 하는 과정이다.

이번 챕터에서는 parameter인 $w^{T}, x$가 linear한 discrimitive model이라는 것을 가정할 것이다. 이렇게 하면 model fitting 과정을 단순화할 수 있다.

Model specification

본격적으로 logistic regression formulation에 대해 알아보자.

$$p(y|{x,w})=\text{Ber}(y|\text{sigm}( w^T x))$$

우리 베르누이 분포를 사용하여 $w^{T}, x$를 sigmoid 함수를 통해 $y$를 추론할 수 있고, 이 과정은 $p(y \mid x, w)$와 같다.

$$ \text{sigmoid}(x) = \frac{1}{1+e^{-x}} $$

Sigmoid 함수의 정의는 위와 같고, 이를 통해 우리는 output을 0과 1 사이의 수로 만들어 줄 수 있다.

위 plot은 2차원 input과 서로 다른 $w$에 대한 $p(y =1 \mid x, w)=\text{sigmoid}(w^{T}x)$를 보여준다.

확률에 대한 boundary를 0.5로 설정하면 linear decision boundary가 유도되며, 이 경계의 법선은 $w$로 지정된다.

Model fitting

이제 우리는 logistic regression model의 parameter를 추정하기 위한 알고리즘에 대해 살펴보자.

MLE

Logistic regression은 베르누이 분포를 이용하기 때문에 이에 대한 NLL (Negative Log-Likelihood)는 다음과 같이 주어진다.

$$ \text{NLL}(w)=-\sum_{i=1}^{N}\log\left[\mu_i^{\mathbb{I}(y_i=1)}\times(1-\mu_i)^{\mathbb{I}(y_i=0)}\right]\\ = -\sum_{i=1}^{N}\left[y_i\log\mu_i+(1-y_i)\log(1-\mu_i)\right] \\ \begin{cases} y_{i} = 1, \ \sum_{i=1}^{N}[y_{i}\log(\mu_{i})] \\ y_{i} = 0, \ \sum_{i=1}^{N}[(1-y_{i})\log(1-\mu_{i})] \end{cases} $$

위 식을 cross-entropy error function이라고도 부른다.

우리는 위 function을 통해 $y$가 0 또는 1일 때에 값을 얻을 수 있다.

또한 해당 함수에 대한 최적화 값 $\frac{\partial}{\partial{w}}\text{NLL}({w})=0$가 되는 $w$를 찾아야 하기 때문에 $\text{NLL}$을 다음과 같이 표현할 수 있다.

$$\begin{cases} p(y=+1)=\frac{1}{1+\exp(-{w}^T{x})}\\ p(y=-1)=\frac{1}{1+\exp(+{w}^T{x})} \end{cases} $$

기존 $y_{i}$를 +1, -1로 표현하였고, sigmoid 함수에 넣은 값이다. 이를 통해 $\text{NLL}$를 풀어쓰면 다음과 같다.

$$\text{NLL}({w})=\sum_{i=1}^{N}\log\left(1+\exp(-\tilde{y}_i{w}^T{x}_i)\right) $$

위 수식에 대해 편미분을 진행해야하지만 logistic regression에서는 closed form solution이 존재하지 않는다. 따라서 optimization algorithm을 적용해서 $w$를 구해야 한다. 여기서 필요한 개념이 gradient, hessian이다.

$${g}=\frac{d}{d{w}}f({w})=\sum_{i}(\mu_i-y_i){x}i={X}^T({\mu}-{y})\\ {H}=\frac{d}{d{w}}{g(w)}^T=\sum_i(\nabla{w}\mu_i){x}i^T=\sum{i}\mu_i(1-\mu_i){x}_i{x_i}^T\\ ={X}^T{SX} $$

Gradient 수식에서 $x^{T}$는 feature matrix를 의미하고, $\mu$는 $p(y=1)$인 경우, $y$는 class를 구분하는 label vector이다.

Hessian 수식에서 $S$는 diagonal matrix로 다음과 같이 정의한다.

$${S}\triangleq\text{diag}(\mu_i(1-\mu_i)) $$

여기서 Hessian은 positive definite를 만족하기 때문에 $\text{NLL}$은 convex이며, convex의 정의에 따라 unique global minimum 값을 갖는다.

여기서 positive definite는 $\forall {x}\in R^N,{x}^T{Hx}\gt0$을 만족하는 것을 의미한다.

Gradient Descent (Steepest Descent)

Unconstrainted optimization을 위한 가장 간단한 알고리즘은 Steepest Descent로 잘 알려진 Gradient Descent이다. 이는 다음과 같이 작성할 수 있다.

$$ \theta_{k+1}=\theta_k-\eta_k{g}_k $$

여기서 $\eta_{k}$는 step size 또는 learning rate를 의미하고, $g_{k}$를 통해 갱신에 대한 방향성을 결정한다. Gradient Descent에서 가장 큰 issue는 step size을 어떻게 결정해야 되는지이다. step size가 작으면 작게 갱신이 되고, 크면 이상한 방향으로 갱신될 수 있다.

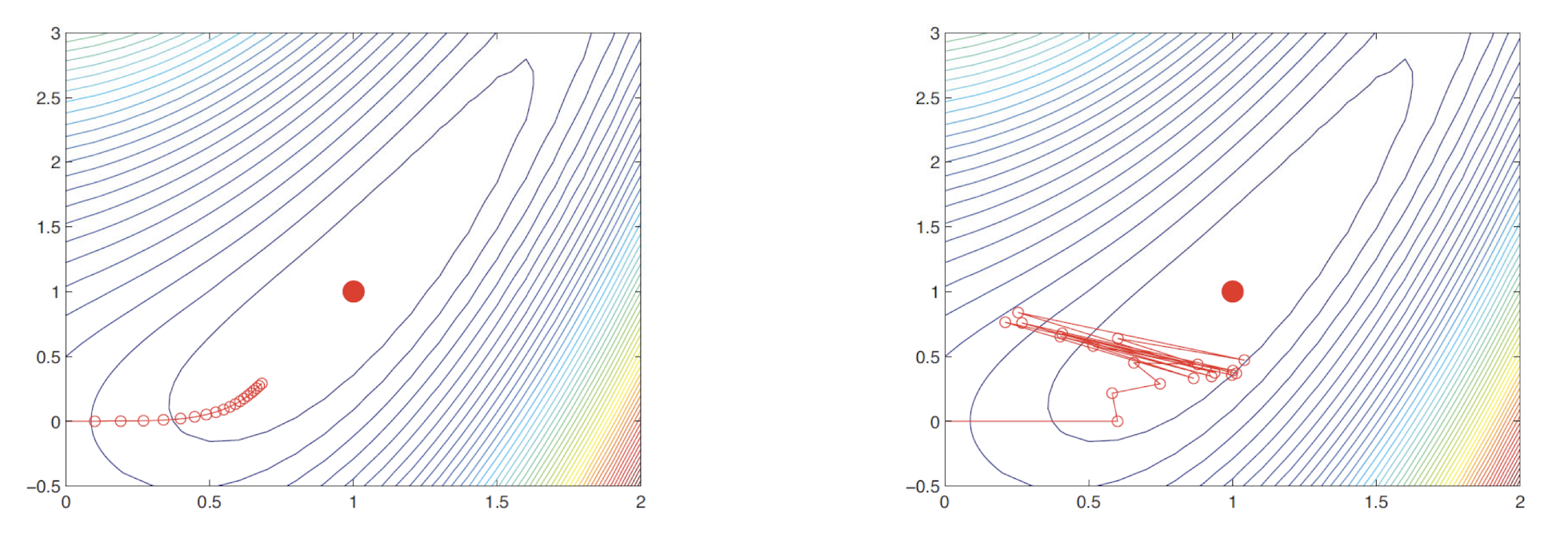
왼쪽 plot은 step size가 0.1인 경우고, 오른쪽은 0.6인 경우이다. 오른쪽과 같이 최적화 지점에 도달하지 못하는 경우를 over shooting이라고 부른다.

특정 step size를 선택하지 않고, 어디에서 시작하는지에 상관 없이 local optimum으로 convergence를 보장하는 stable method에 대해 알아보자. 이러한 속성을 global convergence라고 하고, global optimum과는 다르다.

Tayler’s theorem에 따라 다음 point의 위치를 다음과 같이 쓸 수 있다.

$$f(\theta+\eta{d})\approx f(\theta)+\eta{g}^T{d} $$

여기서 $d$는 descent direction이다. 따라서 $\eta$가 충분히 작게 선택이 된다면 기울기가 음수가 되기 때문에 $f(\theta + \eta d) <f(\theta)$가 된다. 하지만 $\eta$가 너무 작을 경우 매우 천천히 이동하게 돼서 optimal 지점에 도달하지 못하게 된다. 따라서 식을 최소화하는 $\eta$를 찾자.

$$ \phi(\eta)=f(\theta_k+\eta{d}_k) $$

즉, $f(\theta_{k+1}) < f(\theta_{k})$를 만들어주는 $\eta$를 선택한다는 의미이다. 이러한 방법을 line minimization 또는 line search라고 부른다.

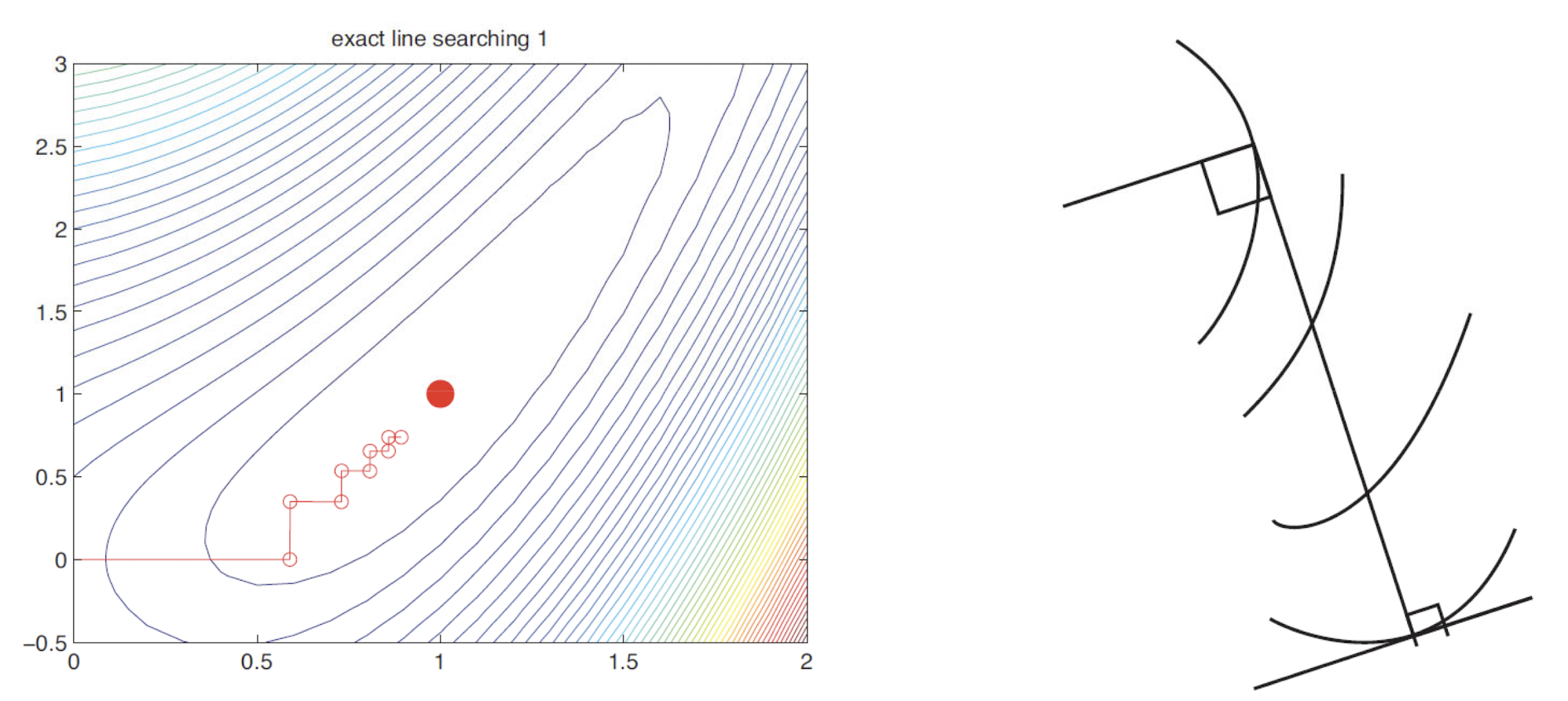
왼쪽 plot은 line search가 실제로 잘 동작하는 것을 보여준다. 하지만 exact search를 하는 steepest descent 경로는 zig-zag와 같은 특성을 보인다. 이러한 이유를 알기 위해 exact line search가 $\eta_{k} =argmin_{\eta>0}{\phi(\eta))}$를 충족한 다는 것에 주목해보자. optimum을 위한 필요충분조건은 $\phi'(\eta)=0$이다.

Chain-rule에 의해 $\phi'(\eta)={d}^T{g}$ 이고, 여기서 $g = f'(\theta + \eta d)$는 step 종료 시의 gradient이다. 따라서 stationary point를 찾았음을 의미하는 $g=0$ 또는 local gradient가 search direction에 perpendicular인 point에서 exact search가 중지됨을 의미하는 $g\ \bot\ d$를 갖는다. 그러므로 연속적인 방향은 위 plot과 같이 orthogonal으로 zig-zag를 설명할 수 있다. 따라서 위와 같이 이동하기 때문에 optimum에 도달하는데 시간이 오래 걸린다는 단점이 존재한다.

이러한 zig-zag를 줄이기 위한 효과적인 방법은 간단한 heuristic으로 momentum term을 추가하면 된다.

$$\theta_{k+1}=\theta_k-\eta_k{g}k+\mu_k(\theta_k-\theta{k-1}),\enspace0\le\mu_k\le1 $$

여기서 $\mu_{k}$는 momentum term의 importance를 조절한다. optimization community에서는 이러한 방법을 heavy ball method라고 한다.

또 다른 방법은 conjugate gradient가 있다. 이 방법은 linear system을 해결할 때 발생하는 $f(\theta) = \theta^{T}A\theta$ 형식의 quadratic objective에 대해 선택하는 방법이다. 이외에도 positive definite을 만족하는 hessian이 존재할 때 이를 이용하는 Newton’s method, IRLS, Quasi-Newton method 등이 존재한다.

 

L2 regularization

Linear regression에서 MLE를 이용하여 model parameter를 구할 때는 $w$가 너무 커지는 문제가 발생할 수 있다고 언급했다. 이러한 문제는 logistic regression에서도 동일하게 발생하는데, 이를 해결하기 위해 $l_{2}$ regularization을 사용한다.

ridge regression에서도 $\Vert w\Vert_2^2$ ($l_{2}$ norm)과 같이 $w$를 조절하기 위해 사용했던 방법으로, logistic regression을 할 때, 데이터가 많아질수록 반드시 필요한 과정 중 하나이다.

그 이유는 데이터가 선형적으로 분리가 가능하면 MLE를 통해 얻어진 parameter $w$에 대해 $\Vert w \Vert \rightarrow \infty$ 인 상황이 발생하게 되는데, 이러한 경우 Linear threshold unit이라고 하는 infinitely steep sigmoid function이라고 불리는 $\mathbb{I}(w^T x\gt w_0)$ 가 발생한다. 이는 학습 데이터의 probability mass의 maximal amount를 할당하게 된다. 따라서 overfitting을 야기하여 학습이 올바른 방향으로 진행되지 않는다.

위 상황들을 방지하기 위해 $l_{2}$ regularization을 사용하고 식은 다음과 같다.

$$ f'(w)=\text{NLL}(w)+\lambda w^Tw $$

위 식에서 2번째 term인 $\lambda$가 속해져 있는 부분이 $l_{2}$ regularization이다.

$$ g'(w)={g(w)}+\lambda w $$

Gradient에는 위 수식과 같이 적용할 수 있다.

$$ H'(w)={H(w)}+\lambda I $$

또한 hessian에 대해서도 적용할 수 있다. 여기서는 identity matrix $I$를 넣어 행렬의 덧셈 연산이 가능하도록 만들어 준다.

이렇게 수정된 수식을 이용하면 $w$가 지나치게 커지는 것을 방지할 수 있다.

 

Multi-Class Logistic Regression

지금까지는 binary class logistic regression에 대해 살펴보았다. 지금부터는 조금 더 general 한 multi-class logistic regression에 대해 살펴보자. 이는 maximum entropy classifier라고도 불리며, model의 수식은 다음과 같다.

$$ p(y=c|x,W)=\frac{\exp(w_c^Tx)}{\sum_{c'=1}^C\exp(w_{c'}^Tx)} $$

우측 항과 같이 약간의 변형을 주어 softmax 형태로 사용할 수 있는데, 이를 conditional logit model이라고 부른다. 이는 각 data class에 대해 서로 다른 class를 normalize 한다. 분모는 서로 다른 class의 합이기 때문에 normalize 하는 효과를 얻을 수 있다.

Multi-class logistic regression의 log-lilkelihood를 구하기 위해 몇가지 Notation을 살펴보자.

$$ \mu_{ic}=p(y_i=c|x_i, W)=\mathcal{S}(\eta_i)_c $$

여기서 $\eta$는 $W^{T}x_{i}$로 표현되고, $W$가 real domain이면 $D \times C$ 차원이 된다. 또한 $x_{i}$는 $D$차원이 된다.

따라서 $\eta$는 $W$와 $x$의 선형 결합으로 표현할 수 있다.

여기서 $y_{i}$는 bit vector이고, 참인 $c$ 값을 만나면 1이 된다.

$W$에 대해 정리를 하면 다른 논문에 의해 0으로 가정한다. 그리고 나머지 $W$의 1부터 $c-1$ 벡터에 대해서만 고려할 텐데, 우리는 $D$를 곱해줌으로 column vector를 만든다.

 

이를 이용하여 $W$에 대한 loss를 얻기 위해 log-likelihood를 다음과 같이 구한다.

$$ \ell(W)=\log\prod_{i=1}^N\prod_{c=1}^C\mu_{ic}^{y_{ic}}=\sum_{i=1}^N\sum_{c=1}^Cy_{ic}\log\mu_{ic} $$

여기서

$$ \mu_{ic}=\frac{\exp(w_c^Tx_i)}{\sum_{c'=1}^C\exp(w_{c'}^Tx_i)}=\mathcal{S}(\eta_i)_c $$

이렇게 표현이 가능함으로, 이를 log-likelihood 식에 적용하면 아래와 같다.

$$ \ell(W)=\sum_{i=1}^N\sum_{c=1}^Cy_{ic}\log\left(\frac{\exp(w_c^Tx_i)}{\sum_{c'=1}^C\exp(w_{c'}^Tx_i)}\right)\\ =\sum_{i=1}^N\left[\left(\sum_{c=1}^Cy_{ic}w_c^Tx_i\right) -\log\left(\sum_{c'=1}^C\exp(w_{c'}^Tx_i) \right)\right] $$

위 식에 -만 붙여 $\text{NLL}$ 식으로 만들면 된다.

$$f(w)=-l(w) $$

Multi-class logistic regression의 gradient와 Hessain을 구하기 위해서는 사전적 수학 지식이 필요하다.

 

Kronecker product

$A$가 $m \times n$인 행렬이고, $B$가 $p \times q$인 행렬이라고 할 때, $A \times B$는 Kronecker product에 의해 $mp \times mq$를 만족하는 block-structured matrix가 된다.

$$ A\otimes B= \begin{bmatrix} a_{11}{B}&\cdots&a_{1n}{B}\\ \vdots&\ddots&\vdots\\ a_{m1}{B}&\cdots&a_{mn}{B} \end{bmatrix} $$

이를 사용하여 gradient와 hessian을 구하게 되면, 아래 식과 유사하게 구할 수 있다.

$$ {g}=\frac{d}{d{w}}f({w})=\sum_{i}(\mu_i-y_i){x}i={X}^T({\mu}-{y})\\ {H}=\frac{d}{d{w}}{g(w)}^T=\sum_i(\nabla{w}\mu_i){x}i^T=\sum{i}\mu_i(1-\mu_i){x}_i{x_i}^T\\ ={X}^T{SX} $$

Multi-Class Logistic Regression’s Gradient

Multi-class logistic regression의 gradient는 kronecker product를 이용하여 다음과 같이 정의한다.

$$ g(W)=\nabla f(w)=\sum_{i=1}^N(\mu_i-y_i)\otimes x_i $$

실제로 3 term에 있는 $\sum$에 대한 formation은 binary class logistic regression에서 정의했던 $g( w)=\sum_{i}(\mu_i-y_i){x}_i$과 굉장히 유사한 것을 확인할 수 있다.

 

여기서 $y_i=(\mathbb{I}(y_i=1),\dots,\mathbb{I}(y_i=C-1))$를 만족하고, $\mu$는 아래 수식을 만족하는 column vector이다.

$$ \mu_i(W)=[p(y_i=1|x_i,W),\dots,p(y_i=C-1|x_i,W)] $$

예를 들어 feature의 dimension이 3이고, $C= 3$이라면 $g(W)$는 다음과 같이 구할 수 있다.

$$ g(W)=\sum_i \begin{pmatrix} (\mu_{i1}-y_{i1})x_{i1}\\ (\mu_{i1}-y_{i1})x_{i2}\\ (\mu_{i1}-y_{i1})x_{i3}\\ (\mu_{i2}-y_{i2})x_{i1}\\ (\mu_{i2}-y_{i2})x_{i2}\\ (\mu_{i2}-y_{i2})x_{i3}\\ \end{pmatrix} $$

결과적으로 각 class $c$에 대해 weight의 $c$ 번째 column에 대한 derivative는 다음과 같이 표현할 수 있다.

$$ \nabla_{w_c}f(W)=\sum_i(\mu_{ic}-y_{ic})x_i $$

Multi-Class Logistic Regression’s Hessian

Hessian은 NLL를 2번 derivative하여 구할 수 있다.

$$ H(W)=\nabla^2f(w)=\sum_{i=1}^N(\text{diag}(\mu_i)-\mu_i \mu_i^T)\otimes(x_i x_i^T) $$

앞과 같은 조건의 예시로 $H(W)$를 구하면 다음과 같다.

$$ H(W)= \sum_i\begin{pmatrix} \mu_{i1}-\mu_{i1}^2&-\mu_{i1}\mu_{i2}\\ -\mu_{i1}\mu_{i2}&\mu_{i2}-\mu_{i2}^2 \end{pmatrix}\otimes\begin{pmatrix} x_{i1}x_{i1}&x_{i1}x_{i2}&x_{i1}x_{i3}\\ x_{i2}x_{i1}&x_{i2}x_{i2}&x_{i2}x_{i3}\\ x_{i3}x_{i1}&x_{i3}x_{i2}&x_{i3}x_{i3}\\ \end{pmatrix}\\ =\sum_i\begin{pmatrix} (\mu_{i1}-\mu_{i1}^2){X}i&-\mu{i1}\mu_{i2}{X}i\\ -\mu{i1}\mu_{i2}{X}i&(\mu{i2}-\mu_{i2}^2){X}_i \end{pmatrix} $$

여기서 $X_{i} = X_{i}X_{i}^{T}$이다.

다르게 보면 block $c$는 $c'$의 sub matrix로 다음과 같이 주어진다.

$$ H_{c,c'}(W)=\sum_i\mu_{ic}(\delta_{c,c'}-\mu_{i,c'})x_ix_i^T $$

여기서 $\delta_{c,c'}$는 두 $c$와 $c'$가 같을 때, $\delta$ 함수가 활성화된다.

또한 위 식은 positive definite 한 matrix 이므로 unique 한 $\text{MLE}$가 존재하기 때문에, 이를 최소화하여 $l_{2}$ regulization을 구할 수 있다.

$$ f'(W)\triangleq-\log{p(D \mid W) - \log{p(W)}} $$

식이 위처럼 주어진다면 $p(W)$는 아래 수식과 같다.

$$ p(W)=\prod_c\mathcal{N}(w_c|0,V_0) $$

각 $w_{c}$라는 column vector는 normal distribution을 따르며, 자세하게 말한다면 multivariate normal distribution을 따른다고 할 수 있다. 여기서 $V_{0}$는 covariance matrix이다.

이렇게 새로 구한 objective function의 gradient와 Hessian은 다음과 같이 주어 진다.

$$ f'(W)=f(W)+\frac{1}{2}\sum_cw_cV_0^{-1}w_c\\ g'(W)=g(W)+V_0^{-1}(\sum_c w_c)\\ H'(W)=H(W)+I_C\otimes V_0^{-1} $$