Bayesian Concept Learning

Introduction

Discrete classification은 크게 Discriminative approach와 Generative approach로 나뉜다.

Discrimitive approach

$$ p(y = c \mid x, \theta) $$

어떠한 model $\theta$가 주어졌을 때, feature vector $x$를 통해 $y=c$인 class를 추론하는 것으로 대표적으로 Linear regression과 Logistic regression이 있다.

Generative approach

$$ p(y=c|x,\theta)\propto p(x|y=c,\theta)p(y=c|\theta) $$

수식은 discrimitive approach와 같지만, 해당 식을 이용하여 바로 추론하는 것이 아니라, Bayes rule을 이용하여 얻어낸 식을 통해 추론을 전개한다.

위 식에서 $p(x|y=c,\theta)$는 conditional density로 $\theta$에 대해 어떤 class의 label이 c일 경우 $x$를 어떻게 나타낼 것인가를 의미한다.

이러한 model을 사용하는 것의 핵심은 class-conditional density에 적합한 형식을 지정하는 것이며, 이는 각 class에서 어떤 종류의 데이터가 표시될 것으로 예상하는지 정의한다.

이번 포스트에서는 관찰된 데이터가 discrete한 경우에 초점을 두며, 이러한 model의 $\theta$를 추론하는 방법에 대해 알아볼 것이다.

 

Bayesian concept learning

심리학 연구에 따르면 사람들은 오직 positive example에서 concept를 학습한다고 한다. 이는 만약 사과라는 물체가 있으면 빨간색, 동그란 모양 등등으로 사과에 대한 concept을 학습한다는 것이고, 노란색이 아닌 것, 사각형이 아닌 것 등으로 사과의 concept을 학습하지 않는다는 것을 의미한다.

이를 통해 concept learning은 어떠한 $x$가 concept $C$의 샘플이면 $f(x) = 1$로 정의하고, 아니라고 하면 $f(x) = 0$이라고 할 수 있다. 이를 통해 집합 $C$의 elements를 정의하는 function $f$를 학습하는 것이다.

Number game

concept learning을 쉽게 이해하기 위해 number game이라는 예시를 살펴보자.

이 game은 다음과 같이 진행 된다.

먼저 prime number 또는 1과 10 사이의 정수와 같은 몇 가지의 Arithmentical concept $C$를 선택한다.

그런 다음 $C$에서 무작위로 추출된 positive example의 series $D = \{x_{1}, \dots, x_{M}\}$을 제공하고, 일부 새로운 test case $\tilde{x}$가 concept $C$에 속하는지 여부를 확인한다. 즉 $\tilde{x}$를 classify 하도록 요청한다.

위 그림의 예시와 같이 모든 숫자가 1과 100 사이에 있는 정수라고 가정하자. 16이라는 숫자가 concept의 positive example이라고 한다면 다른 positive인 숫자는 무엇일까?

하나의 example 만으로는 예측하기 힘들다. 다른 의미로 본다면 첫 번째 plot과 같이 16과 근처에 있는 수들이 가능성이 높다고 생각할 수 있다. 또한 16의 배수인 32, 64, 96도 가능성이 높은 것도 확인할 수 있다.

positive example이 많아 질 수록 아래 있는 plot들과 같이 다른 postive case에 대해 더욱 명확하게 추론하는 것을 확인할 수 있다.

이것을 확률 분포로 $p(\tilde x|D)$로 표현할 수 있고, 이것은 $\tilde x \in C$ 가 $\forall\tilde x\in\{1,\dots,100\}$ 에 대해 데이터 $D$를 제공할 확률이다.

이를 Posterior predictive distibution이라고 한다.

Conecept learning에서 우리는 위 예시에서 홀수, 짝수, 1과 100 사이의 수, 16의 배수와 같은 concept space $H$가 있다고 가정하는 것이다.

이와 더불어 데이터 $D$와 일치하는 $H$의 subset을 version space라고 한다.

즉 더 많은 example을 볼 수록, version space는 줄어들고, concept에 대해 점점 더 확신하게 된다.

하지만 version space가 전부는 아니다. $D=\{16\}$ 을 보고 나면 일관된 규칙이 매우 많이 존재한다. $\tilde x \in C$인지 예측하기 위해 이러한 규칙들을 결합하여 사용할 수 있다.

$D = \{ 16, 8, 2, 64\}$가 주어진다면 이것이 왜 짝수, 32를 제외한 2의 제곱이 아닌 2의 제곱이라는 규칙이 존재한다고 생각할까? 이를 위해 아래를 통해 자세히 알아보자.

Likelihood

concept의 extension에서 example이 무작위로 균등하게 sampling 된다고 가정하자. 여기서 extention은 concept에 속하는 set of number를 의미한다. 예를 들어 $h_{\text{even}}$은 $\{ 2,4, 6, \dots, 100 \}$이다.

이를 수학적으로 추론하기 위해 Strong sampling assumption을 이용한다.

assumption이 주어지면 $h$에서 대체할 수 있는 $N$개의 item을 independently sampling 할 확률은 다음과 같다.

$$ p({D}|h)=\left[\frac{1}{\text {size}(h)}\right]^N=\left[\frac{1}{|h|}\right]^N $$

model은 data와 일치하는 가장 작은 hypothesis를 선호한다. 이는 occam’s razir로 더 잘 알려져 있다.

위 수식이 어떻게 동작하는지 알아보기 위해 $D= \{ 16\}$이라고 가정하자.

그러면 100보다 작은 2의 제곱이 6개이기 때문에 $p(D \mid h_{two}) = \frac{1}{6}$이고, 50개의 짝수가 있기 때문에 $p(D \mid h_{even}) = \frac{1}{50}$이다. 따라서 $h = h_{two}$의 likelihood는 $h= h_{even}$인 경우보다 더 크다. 4개의 example $D = \{ 16, 8, 2, 64\}$에 대해 $h_{two}$의 likelihood는 $(\frac{1}{6})^{4} = 7.7 \times 10^{-4}$이고, 반면 $h_{even}$의 likelihood는 $(\frac{1}{50})^{4} = 1.6 \times 10^{-7}$이다. 이는 $h_{two}$가 선호되는 것에 대해 5000 : 1의 likelihood ratio이다. 이러한 결과는 $D = \{ 16, 8, 2, 64\}$가 $h_{even}$에 의해 생성된 경우 supicious coincidence가 될 것이라는 key intuition을 수학적으로 증명한 것이다.

 

Prior

Prior는 사전 지식의 깊이를 의미하고, 이것이 많을수록 rapid 한 learning이 가능하다. 작은 sample size로부터 이러한 prior가 존재하지 않는 다면 학습이 어려울 수도 있다.

prior는 방금 언급한 것처럼 사전 지식이 중요하다.

$D= \{ 1200, 800, 900, 1400\}$이라는 data set이 주여 졌을 때 $400$에 대한 prior는 무엇일까?

concept이 100의 배수라고 하면 prior가 높을 수 있지만, $400$이 아닌 $1183$과 같은 수는 낮을 수 있다.

$H$가 건강 수치하고 한다면 $1183$에 대해 prior를 더 높게 줄 수 있다.

만약 적절한 prior가 없으면 uniform과 같은 simple prior를 통해 안정성을 줄 수 있다고 한다.

Posterior

Hypothesis의 posterior를 생각해보면 아래 수식과 같이 bayes rule을 적용하여 쓸 수 있다.

$$ p(h \mid D) = \frac{p(D \mid h)p(h)}{\sum_{h' \in H}p(D, h')} = \frac{\frac{p(h)I(D \in h)}{\mid h \mid^{N}}}{\sum_{h' \in H}{\frac{p(h')I(D \in h')}{\mid h' \mid^{N}}}} $$

Term 2에 수식을 조금 더 확장하면 아까 언급했던 size principle을 통해 likelihood를 indicator function으로 쓸 수 있다 $h$에 속하면 $h$의 size 만큼 $N$ 제곱만큼 커지는 것도 이전에 다뤘던 내용이다.

여기서 $p(h)$는 prior이다. 이러한 posterior는 likelihood에 의존적이다.

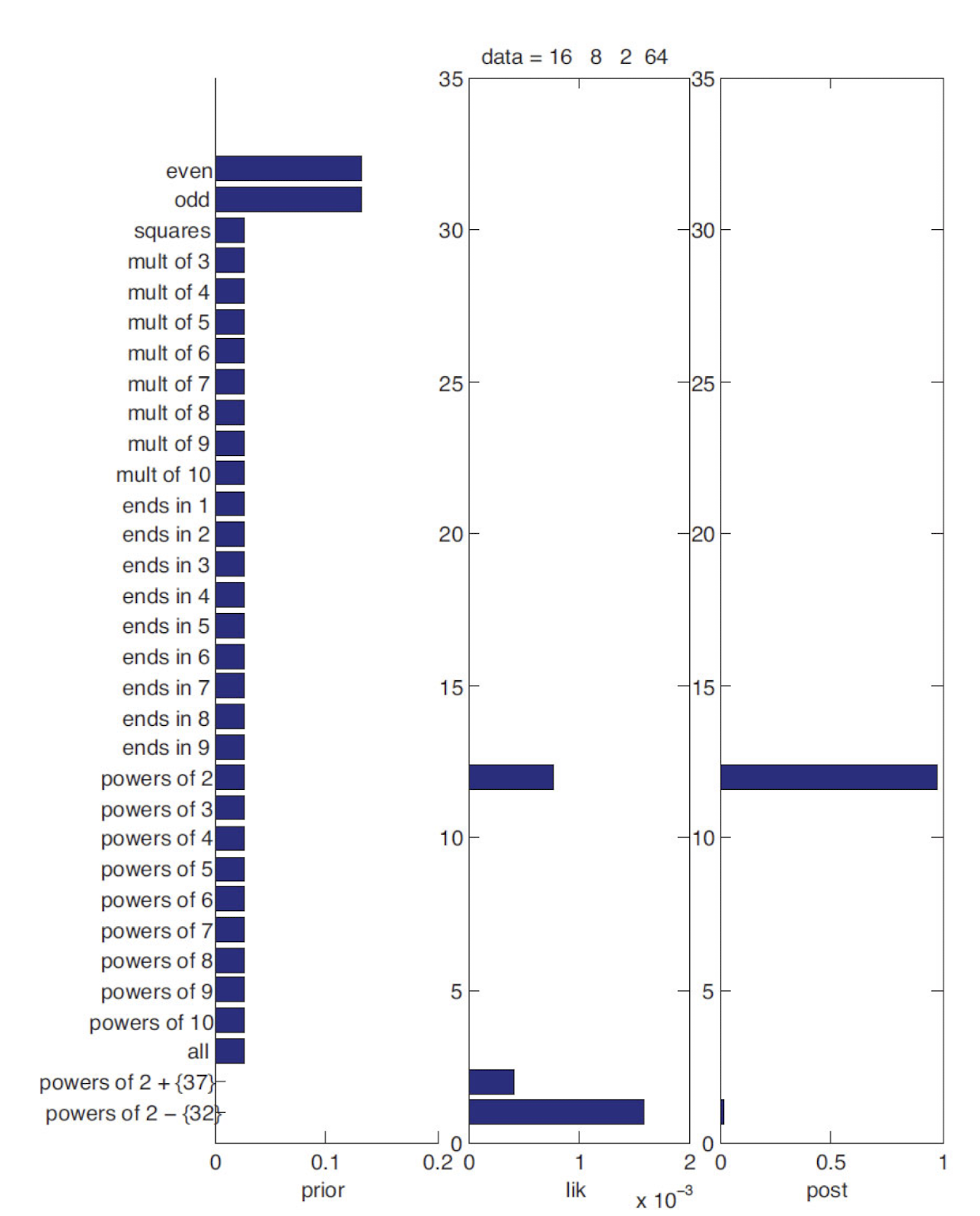
위 plot과 같이 자연스럽지 않은 prior를 낮게 줄 수 있다. (맨 아래 2개)

우리는 prior와 likelihood를 통해 어떤 $H$에 대해 확률이 가장 높은지 알 수 있다.

이를 통해 알 수 있는 사실은 sample들이 많이 주어지면 hypothesis의 경우의 수는 줄어든다. 따라서 sample이 많을수록 posterior는 수렴하게 되고, 이를 통해 가능성 있는 hypothesis를 명확하게 구할 수 있게 된다. 결과적으로 하나의 concept로 수렴하게 된다.

이를 수식으로 표현하면 다음과 같다.

$$ p(h \mid D) \rightarrow \delta_{\hat h^{\text{MAP}}}(h) \\ \hat h^{\text{MAP}} = argmax_{h}(h \mid D): \text{posterior mode} \\ \delta = \begin{cases} 1 \ \ \text{if} \ x \in A \\ 0 \ \ \text{if} \ x \notin A \end{cases} $$

위 식과 같이 어떠한 sample $x$가 정답 hypothesis space인 $A$에 속하면 1 아니면, 0으로 쓸 수 있고, $\hat h^{MAP}$는 likelihood와 prior로 바꿔서 쓸 수 있다.

$$ \hat h^{MAP} = argmax_{h}p(h \mid D)p(h) = argmax_{h}[\log{p(D\mid h) + \log p(h)]} $$

$MAP$는 Maximum a posterior의 줄임말인데, 이는 최대로 하는 posterior, 즉 hypothesis를 찾는다.

$MAP$는 데이터의 개수가 증가함에 따라 $MLE$로 바꿀 수 있다. 그 이유는 데이터가 많으면 prior에 영향이 적어지기 때문이다.

$$ \hat h^{MLE} = argmax_{h}p(h \mid D) = argmax_{h}{\log p(D \mid h)} $$

True hypothesis가 hypothesis space에 존재한다면 MAP/ML 추정치가 해당 hypothesis에 수렴이 된다.

이를 통해 무한한 데이터의 한계에서 truth를 통해 recover 할 수 있으며, 이를 일반화하면 가능한 한 truth에 가까운 hypothesis를 수렴할 수 있다는 것이다.

 

Posterior Predictive distribution

우리는 hypothesis를 결정하기 위해 posterior predictive distribution을 만들어야 하는데, 이를 구하는 것이 가장 어렵니다.

이를 구하기 위해 Bayes model averaging을 알아보자.

$$ p(\tilde x \in C \mid D) = \sum_{h} p(y = 1 \mid \tilde x, h)p(h \mid D) $$

$D$는 train dataset이고, $\tilde x$는 test sample이다. 이를 통해 distribution과 이에 대응하는 확률을 위 수식을 통해 구할 수 있다.

$p(h \mid D)$는 posterior이고, 이를 구하려면 likelihood와 prior도 구해야 한다.

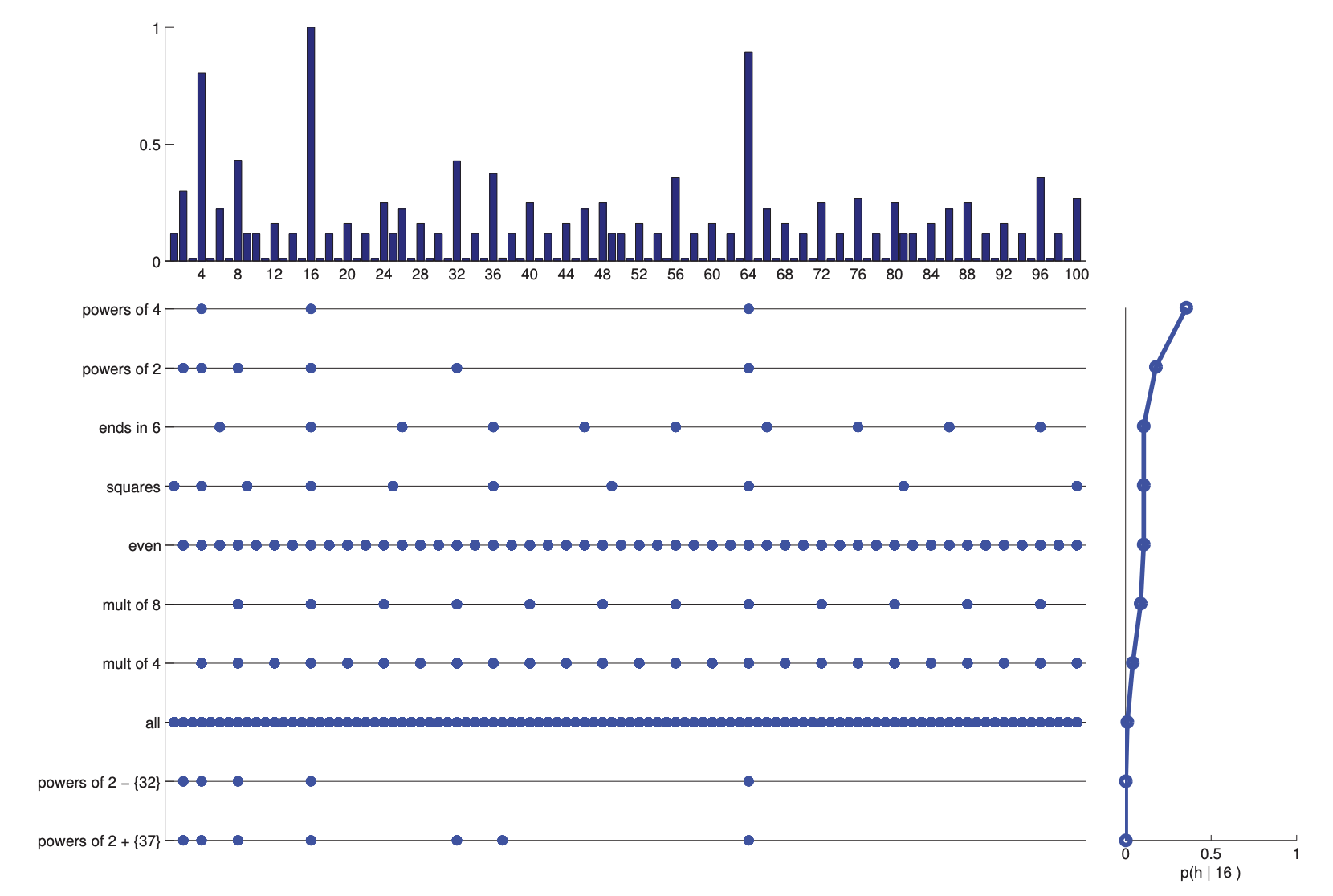
$\sum$은 posterior에 대한 wieight라고 생각하면 된다. 위 plot을 보며 이해를 해보면 16이라는 정수 sample이 주어졌다고 가정하자. 이에 대한 posterior $p(h \mid 16)$은 맨 오른쪽 plot과 같다. 왼쪽 plot의 point는 hypothesis에 의해 생성될 수 있는 숫자들이다. 이는 수식에서 $\sum_{h} p(y=1 \mid \tilde x, h)$와 같다. 각 hypothesis에 속하는 point의 생성 확률을 나타낸 것은 맨 위 plot과 같다. 이는 $p(\tilde x \in C \mid D)$와 같다.

맨 위 plot을 통해 16, 64와 같은 sample들이 생성될 확률이 높게 나오는 것을 확인할 수 있다.

데이터가 적고 quality가 낮으면 posterior predictive distribution은 broad 하게 나온다. 이는 모든 경우에 대해 확률이 넓고 균등하게 나온다는 것이다.

이런 case를 보완하기 위해 plug-in approximation을 도입할 수 있다. plug-in approximation은 predictive distribution의 대한 계산을 수월하게 하기 위해 잘 알려지지 않은 parameter를 MLE로 대체하는 기법이다.

$$ p(\tilde x \in C \mid D) = \sum_{h} p(\tilde x \mid h)\delta_{\tilde h}(h) = p(\tilde x \mid \hat h) $$

hypothesis의 불확실성을 줄이기 위해 posterior를 MAP estimation 역할을 하는 $\delta$ function으로 대체한다.

$\sum$ term에 있는 수식은 posterior가 가장 큰 $h$만 고려해서 구할 수 있다. 이를 통해 $p(\tilde x\mid \hat h)$로 표현할 수 있고, 이는 likelihood와 동일한 형태이다.

이러한 approximation은 불확실성을 under represent 하였기 때문에 non-smooth 하다. 이 말은 즉슨 $h$를 잘 선택하면 좋지만, 이상한 $h$를 선택한다면 성능이 좋지 않다는 의미이다.

Complex prior

산술적으로 구한 prior에 더해서, 정수 $n$과 $m$ 사이의 수를 가지고 modeling을 할 수 있지 않을까라는 생각으로 나온 것이 complex prior이다. $(1 \leq n, m\leq 100)$

$$ p(h) = \pi_{0}p_{\text{rules}}(h) + (1-\pi_{0}) p_{\text{interval}}(h) $$

$\pi_{0}$는 상대적인 weight를 의미하고, 0.5 이상으로 정의된다. 이는 hyper parameter이다.

Beta-Binomial Model

이번에는 다른 generative model인 Beta-binomial model에 대해 알아보자.

이전까지 살펴보았던 number game의 문제는 concept에 대한 space가 작지가 않았던 점이다. 이는 parameter를 알지 못하고, 값이 연속적이고, space 자체가 다차원이 될 수 있다는 문제점도 가지고 있다.

이러한 문제점을 보완하고자 조금 더 넓은 영역을 cover 하는 model이 beta-binomail model이다.

 

Likelihood

동전 던지기는 게임을 예로 들어 보자.

단순히 동전을 1번 던지는 경우는 베르누이 분포로 생각할 수 있다. 동전을 $n$ 번 던져 $k$번 나오는 경우를 생각하면 이는 Bionomail distribution으로 확장이 가능하고, 다음과 같은 수식을 따르게 된다.

$$ Bin(k \mid n, \theta) = \left(\begin{array}{c}n\\ k\end{array}\right)\theta^{K}(1- \theta)^{n-k} $$

여기서 $s(D)$를 sufficient statistics라고 하고, 데이터 $D$가 이를 만족한다면 $p(\theta \mid D) = p(\theta \mid S(D))$ 수식을 만족하게 되고, 만약 여기서 uniform prior를 사용한다고 하면 $p(D \mid \theta) = p(s(D) \mid \theta)$도 만족하게 된다. 이를 통해 서로 다른 데이터가 2개 존재할 때 이들이 sufficient statics가 같다면 $\theta$ 즉 확률 값도 같아진다.

Prior

Prior는 likelihood와 form이 유사하다.

$$ p(\theta) \propto \theta^{\gamma_{1}}(1- \theta)^{\gamma_{2}} $$

우리는 binomial distribution을 가지고 modeling을 진행했는데, $\theta$에 대한 prior도 위 수식과 같이 표현된다.

수식에서 $\gamma_{1}, \gamma_{2}$도 prior parameter이다.

위 수식을 조금 더 쉽게 풀어서 사용할 수 있다.

$$ p(\theta) \propto p(D \mid \theta)p(\theta) = \theta^{N_{1}}(1-\theta)^{N_{0}}\theta^{\gamma_{1}}(1- \theta)^{\gamma_{2}} \\ = \theta^{N_{1}+\gamma_{1}}(1- \theta)^{N_{0}+\gamma_{2}} $$

prior와 posterior가 같은 form을 가지고 있을 때, 우리는 prior를 conjugate prior라고 부른다.

conjugate prior는 계산하기 쉽고, 변환에 용이하기 때문에 널리 사용된다.

우리가 위해서 정의한 conjugate prior는 beta 분포를 따른다.

$$ \text{Beta}(\theta \mid a, b) \propto \theta^{\alpha-1} (1- \theta)^{\beta-1} $$

수식에서 $\alpha$와 $\beta$는 hyper parameter이다. Beta distribution은 $\theta$가 0과 1 사이에 존재하고, modeling을 더 쉽게 할 수 있기 때문에 사용한다. 여기서 $\theta$는 사전 지식으로 결정한다.

만약 사전 지식이 존재하지 않는 다면 uniform으로 설정한다.

Posterior

Posterior는 Likelihood $\times$ Prior로 표현이 가능하며, 수식은 아래와 같이 전개된다.

$$ p(\theta \mid D) \propto \text{Bin}(N_{1} \mid \theta, N_{0} + N_{1}) \text{Beta}(\theta \mid a, b) \\ \propto\text{Beta}(\theta \mid N_{1} + a, N_{0} +b) \\ \propto \theta^{N_{1} +a}(1-\theta)^{N_{0} +b} $$