[Anomaly Detection] Gaussian Density Estimation & Mixture of Gaussian Density Estimation

본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다.

 

Gaussian Density Estimation

Density 기반의 anomaly detection의 목적은 abnormal data의 2번째 관점에 맞춰져 있다. 이는 먼저 정상에 대한 데이터의 분포를 먼저 추정한 후 이 분포에 대해 새로운 데이터가 들어오는데, 해당 데이터가 생성될 확률이 높으면 정상으로 판별하고, 낮으면 비정상으로 판별한다.

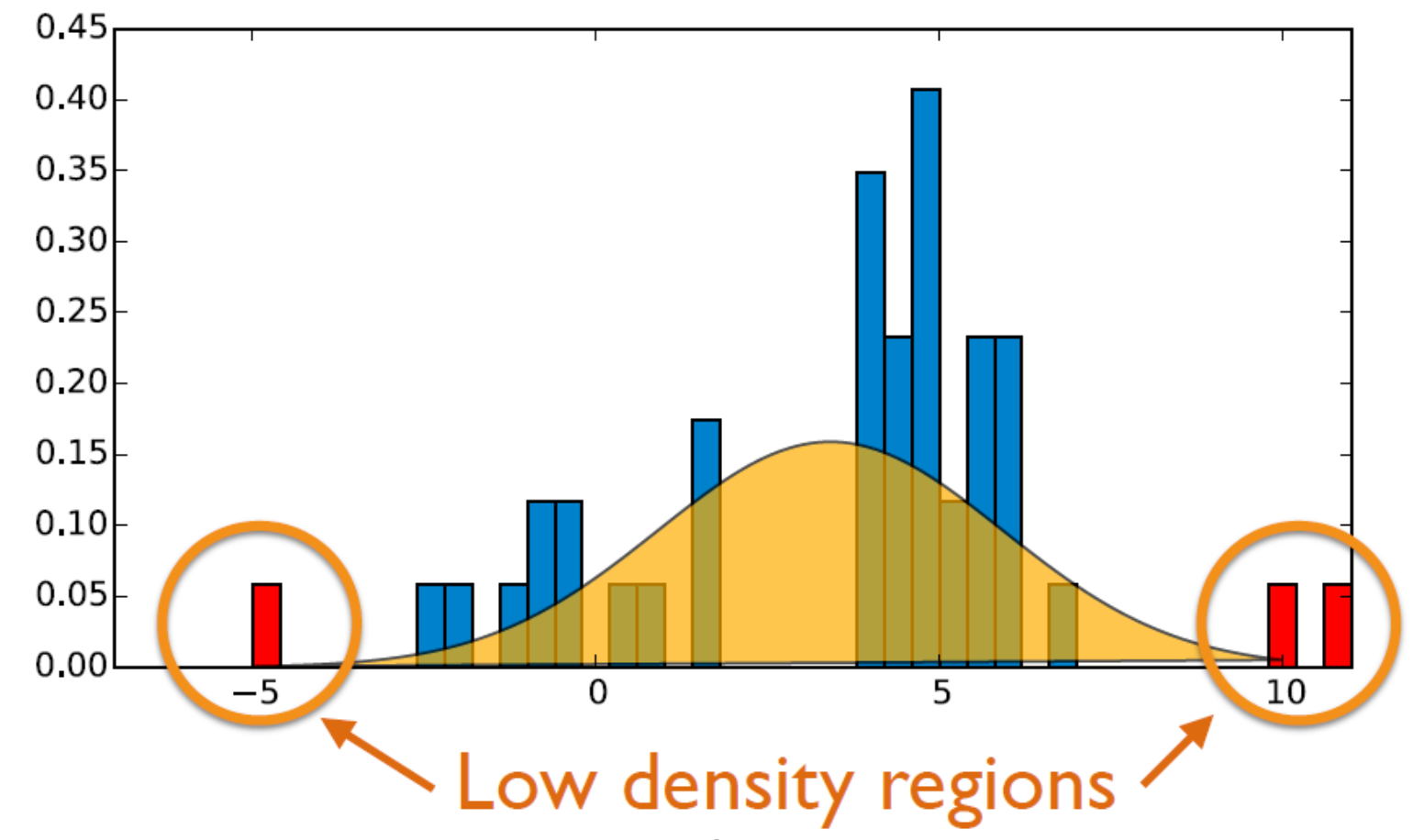
위 그림에서는 데이터의 생성 확률 분포가 Gaussian이라고 가정한다. 새로운 데이터가 들어왔을 때, Gaussian distribution의 $\mu$와 가깝게 생성이 된 경우라면 정상이라고 가정하고, 빨간색 데이터와 같이 일정 확률 이하에서 발생한 데이터라면 비정상이라고 판별한다.

핵심은 데이터로 부터 density function을 추정하는 것이다.

우리가 살펴볼 Gaussian density estimation의 종류는 크게 3가지가 있다. 위 그림은 각 종류에 따른 plot화 된 모습이다.

맨 왼쪽 plot은 Gaussian Density Estimation이며, 이는 전체 데이터가 1개의 Gaussian distribution으로부터 생성되었다고 가정하고 평균 벡터와 공분산 행렬을 estimation 하며 학습을 진행한다.

가운데 plot은 Mixture of Gaussian Density Estimation이며 Gaussian distribution의 개수가 1보다는 크지만, 학습 데이터에 대한 instance보다는 작다고 가정할 때이다. 만약 Gassian distribution과 instance의 수가 같은 경우에는 맨 오른쪽과 같이 Kernel Density Estimation이 되며, 이는 각 instance들은 Gaussian distribution의 중심임을 가정하고, 이로부터 주어진 정상 데이터 영역의 밀도를 추정한다.

1. Gaussian Density Estimation

모든 관측치들은 1개의 Gaussian distribution으로부터 sampling 및 생성이 되었다고 가정한다. 이렇게 된다면 density function이 명확하게 정의된다. 식은 다음과 같다.

$$ p(x) = \frac{1}{(2\pi)^{\frac{d}{2}}\mid \sum \mid^{\frac{1}{2}}}exp\left[ \begin{array}{cc} \frac{1}{2}({x} - \mu)^{T} \sum^{-1}({x} - \mu) \end{array} \right] $$

우리가 위 식에서 찾아야 하는 parameter는 굉장히 많은 ${x}$가 주어졌을 때, $\mu$와 covariance matrix인 $\sum$을 찾으면 된다.

Gaussian density estimation의 첫 번째 장점은 데이터의 범위에 민감하지 않다. 이를 다른 말로 하면 robust인데, 다음과 같이 구성이 되어 있다고 가정하자.

다른 model에서는 해당 element 값들을 scailing 해야지 normalization을 할 수 있다. 하지만 Gaussian에서는 covariance matrix를 구하기 때문에 변수에 대한 측정 단위에 민감하지 않다. 이를 다른 말로 하면 incentive 하다는 것이다. 따라서 값에 대한 normalization 과정이 필요하지 않다.

두 번째 장점은 optimal threshold를 분석적으로 compute 할 수 있다. 이는 예를 들어 신뢰 구간을 95%로 잡을 때 5% 정도는 잘 못 맞춘다고 가정해서 계산을 진행할 수 있다는 의미이다.

다시 말하면 학습 데이터로부터 처음부터 rejection에 대한 1종 오류에 대한 정의를 먼저 할 수 있다.

1차원 데이터로부터 실제로 계산을 해보자. 결국 parameter를 통해 현재 존재하는 데이터를 실제 생성할 가능성이 가장 높은 지를 추정할 수 있다. MLE를 통해 $\mu$와 $\sigma^{2}$에 대해 식을 정의할 수 있다.

데이터는 $i.i.d$라고 가정한다.

$$ L = \prod_{i = 1}^{N}p(x_{i}|\mu, \sigma^{2}) = \prod_{i=1}^{N}\frac{1}{\sqrt{2 \pi}\sigma}exp(-\frac{(x_{i} - \mu)^{2}}{2\sigma^{2}}) \\ LogL = -\frac{1}{2}\sum^{N}{i = 1}{\frac{(x{i} - \mu)^{2}}{\sigma^{2}}} - \frac{N}{2}log(2\pi \sigma^{2}) $$

식을 살펴보면 데이터를 $i.i.d$로 가정하였기 때문에 각 데이터에 대한 확률을 곱해주었다. 또한 $p$에 대한 함수는 위에서 정의한 Gaussian으로 넣어 주었다.

위 식을 최적화하기 위해 각 $\mu$와 $\sigma$에 대한 편미분 값을 0으로 만들어야 한다. 하지만 $\sigma$를 그냥 쓰기에는 계산하기 가 힘들어 $\gamma = \frac{1}{\sigma^{2}}$로 치환하여 계산해보자.

$$ LogL = -\frac{1}{2}\sum^{N}{i = 1}{\gamma(x{i} - \mu)^{2}} - \frac{N}{2}log(2\pi) +\frac{N}{2} log(\gamma)\\ \frac{\partial LogL}{\partial \mu} = \gamma \sum^{N}{i = 1}{(x{i} - \mu)} = 0 \rightarrow \mu = \frac{1}{N} \sum^{N}{i = 1}{x{i}} \\ \frac{\partial LogL}{\partial \gamma} = -\frac{1}{2} \sum^{N}{i = 1} (x{i} - \mu)^{2} + \frac{N}{2 \gamma} = 0 \rightarrow \sigma^{2} = \frac{1}{N}\sum^{N}{i = 1}(x{i} - \mu)^{2} $$

계산을 진행하면 결국 $\mu$는 현재 가지고 있는 train set에 normal sample에 대한 평균값이다.

$\sigma^{2}$ 값은 train set에 normal sample에 대한 분산 값이 된다.

결국 MLE 식은 너무 당연하게도 평균은 정상 데이터에 대한 평균, 분산도 정상 데이터에 대한 분산 값이 나온다.

이를 다차원으로 확장해서 일반화해보면 식은 다음과 같이 나오게 된다.

$$ \mu = \frac{1}{N} \sum^{N}{i=1} {x}{i}, \ \ \ \textstyle \sum = \frac{1}{N}({x}{i} - \mu)({x}{i} - \mu)^{T} $$

위와 같이 평균도 정상 데이터들의 평균이 나오게 되고, covariance matrix도 정상 데이터들의 대한 covariance matrix가 된다.

Gaussian Density Estimation은 normal의 평균과 공분산만 계산하면 되기 때문에 Gaussian 분포식 자체의 시간 복잡도는 constant time이다.

여기서 1가지 issue는 covariance matrix에 대한 결정이다.

Spherical cov matrix를 사용하면 모든 변수가 동일한 분산을 갖는다고 가정을 한 것이다.

오른쪽 그림과 같이 수평 및 수직이면서 원의 형태를 갖는다. 이는 가장 엄격한 가정이다.

만약 cov matrix를 변수들은 독립이긴 한데, 다른 분산 값을 갖는 diagonal cov matrix라고 가정하면 다음과 같다.

여전히 등고선들이 축에 수직 및 수평하지만 타원의 형태를 띠는 것을 볼 수 있다.

모든 cov matrix에 대한 가정을 완화하면 그냥 full cov matrix가 되는데 이는 다음 그림과 같이 보인다.

수직, 수평을 만족하지 못하면서 타원으로 변한 모습을 볼 수 있다

따라서 데이터가 충분히 많고, cov matrix가 not singular matrix이면 full cov를 쓰는 것이 좋긴 하지만 현실적으로 환경적 문제와 noise 문제 등 데이터에 대한 변동성에 대해 잘 맞지 않는 경우가 대다수다.

Gaussian Density Estimation에서 anomaly socre는 $1 - p(x)$로 구한다.

2. MOG (Mixture of Gaussian) Density Estimation

MOG Density Estimation은 기존 Gaussian Density Estimation의 확장판이다. 기존 조건은 데이터의 생성 확률이 unimodal 및 convex 특성을 가져야 한다. 따라서 현실 존재하는 데이터 기준으로는 매우 엄격한 조건이다.

Unimodal 조건을 multi-modal로 확장해서 생각할 수 있는데, 이는 normal distribution의 선형 결합으로 표현할 수 있다. 이를 통해 기존 Gasussian Density Estimation 보다는 더욱 정확한 추정이 가능하지만, 더 많은 수의 데이터가 필요하다.

총 3개의 distribution을 가지고 가중치를 주어 선형 결합을 통해 최종적인 $f(x)$ model을 추정할 수 있다.

이를 수식으로 표현하면 다음과 같다.

$$ f(x) = w_{1} \cdot \mathcal{N}(\mu_{1}, \sigma^{2}) + w_{2} \cdot \mathcal{N}(\mu_{2}, \sigma^{2}) + w_{3} \cdot \mathcal{N}(\mu_{3}, \sigma^{2}) $$

위 식을 통해 우리가 구해야 하는 parameter의 수는 각 distribution의 $\mu_{i}, \sigma^{2}{i}, w{i}$ 가 된다. 여기서 추가적으로 실제 데이터의 distribution이 몇 개의 Gaussian distribution을 사용했는지도 알아야 한다.

MOG의 compoments를 살펴보자. 어떠한 instance가 normal class에 속할 확률을 다음과 같이 정의한다.

$$ p({x} \mid \lambda) = \sum_{m =1}^{M}{w_{m}g({x} \mid \mu_{m}, \textstyle \sum_{m} )} $$

$\lambda$는 위에서 설명한 우리가 추정해야 하는 미지수의 집합이다. $M$은 전체 gaussian의 개수이다.

위 식을 통해 새로운 instance가 normal에 속할 확률 값은 각 gaussian distribution에 대한 Likelihood로 계산한 다음 가중치를 곱한 총 합이 된다.

참고로 $g()$는 앞에서 정의한 Single Gaussian density function의 식이 된다.

이제 이에 대한 최적화를 진행해야 한다. machine learning에서 최적화 기법은 많지만 여기서는 Expectation-Maximization Algorithm을 사용한다.

Expectation-Maximization Algorithm의 설명은 다음과 같다.

이는 어떠한 미지수 $x,y$가 존재할 때 $x, y$는 동시에 최적화할 수 없는 상황이라고 가정한다. 여기서 $x$를 고정시켜두고 $y$에 대해서 최적화를 시킨다. 그 후 $y$를 고정시키고 $x$에 대해 최적화를 진행한다. 이를 반복하다 보면 결국 $x$와 $y$가 최적화 지점에 수렴하게 된다. 이를 통해 한번에 1개에 대한 미지수만 최적화를 진행한다.

MOG에서 우리가 추정해야 하는 것은 $w, \mu, \sigma$가 있다. 이를 추정하기 위한 식은 다음과 같이 정의된다.

$$ p(m\mid {x}{i}, \lambda) = \frac{w{m} g(x_{i} \mid \mu_{m}, \textstyle \sum_{m})}{\sum_{k =1}^{M}{w_{k} g({x}{t} \mid \mu{k}, \textstyle \sum_{k})}} $$

위 식을 통해 ${x}$가 어떠한 gaussian distribution에 속하는지에 대한 확률 값이다. 단순한 조건부 확률이다.

$$ w_{m}^{(new)} = \frac{1}{N}\sum_{i=1}^{N}p(m \mid {x}{i}, \lambda)\\ \mu{m}^{(new)} = \frac{\sum_{i=1}^{N}p(m \mid {x}{i}, \lambda){x}{i}}{\sum_{i=1}^{N}p(m \mid {x}{i}, \lambda)} \\ \sigma^{2 (new)}{m} = \frac{\sum_{i=1}^{N}p(m \mid {x}{i}, \lambda){x}{i}^{2}}{\sum_{i=1}^{N}p(m \mid {x}{i}, \lambda)} - \mu^{2(new)}{m} $$

$p$에 대한 식을 A라고 두고, 위 각 3개의 parameter에 대한 식을 B라고 하자.

A, B에 대해 Expectation-Maximization Algorithm를 적용시킨다. 이를 반복하면서 수렴하는 $w, \mu, \sigma$를 찾을 수 있다.

A 과정을 통해서는 $x$가 몇 번째 gaussian에 속하는지에 대한 확률을 구할 수 있고, B를 통해서는 그나마 optimal 한 parameter를 구할 수 있다.

MOG의 특징은 $w, \mu, \sigma$에 대해서는 완벽한 optimal 값을 구하지는 못하지만 $p$를 통해 몇 번째 gaussian에서 산출되는 것이 optimal인 것을 찾을 수 있다.

MOG도 cov matrix의 type에 따라 결과가 달라진다.

오른쪽으로 갈수록 cov에 대한 조건이 완화가 된다. 완화가 될수록 정밀도가 높아지지만 계산이 더욱 어려워진다.

Full cov matrix를 사용하면 좋지만, 이는 non-singular일 때만 유용한데, 현실 데이터에서는 cov에 대한 역행렬을 구할 때 non-singular인 경우는 거의 없다.

따라서 적절한 Diagonal cov matrix를 사용하는 것이 보편적이다.