[Anomaly Detection] Parzen Window Density Estimation
본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다.
Kernel density estimation
앞서 설명한 Gaussian density estimation, MOG density estimation은 parametric appoach이다. 이는 특정한 parameter를 갖는 distribution을 가정한 상태에서 주어진 data를 해당 distribution에 끼어 맞추는 방법이다. 이를 통해 data들에 대한 평균과 공분산 행렬을 추정한다.
Kernel density estimation은 data가 특정한 distribution으로부터 estimation 되었다는 가정을 하지 않고, Data 자체로부터 sampling 될 확률을 추정한다. 따라서 사전에 정의된 distribution을 따르지 않기 때문에 Non-parametric density estimation이다.
Parametric Models
: Model을 parameter 관점에서 분류할 수 있다. parametric model이란 model이 가지고 있는 parameter들이 미리 정의되어있는 상태에서 fixed parameter를 가지고 학습을 하는 것을 의미한다. parametric model의 장점은 빠르게 동작하며, 구현 난이도가 비교적 쉽다. 하지만 data distribution 자체에 대해 정확하게 추정할 수 있는 알고리즘으로 설계가 되어야 한다.
Non-Parametric Models
: Non-parametric model은 주어진 dataset $D$에 대해 학습하는 model이다. parameter의 수는 train dataset의 양에 따라 가변적이다. 이 때문에 parametric model에 비해 model이 flexible 하다. 하지만 큰 data가 증가하면 train 및 test, inference의 복잡도가 parametric에 비해 상대적으로 증가되고, modeling 난이도 또한 더 어렵다. 또한 dataset의 distribution에 대한 가정 없이 주어진 data만을 가지고 최적의 model을 구하는 방법으로 parameter의 개수도 바뀔 수 있다.

위 그림과 같이 어떠한 데이터도 상관없이 각 single data에 대해 sampling 될 확률을 추정하는 것이 kernel density estimation이다.

위 plot에서 아래 검정색 십자들은 실질적인 데이터들이고, 회색은 실제 데이터에 대한 분포이다. kernel function을 어떠한 얘를 쓰냐에 따라 추정하는 분포가 달라진다.
본격적으로 kernel-density estimation을 이해하기 위한 사전 지식이 필요하다.
어떠한 데이터가 주어졌을 때, 이 데이터는 $p(x)$로부터 sampling 되었고, 이 데이터가 특정한 영역 $R$에 들어올 확률 값은 다음과 같이 수식으로 표현할 수 있다.
$$ P = \int_{R}p(x')dx' $$
이러한 sampling이 $N$번 반복했다고 가정하자. $R.V.$를 $i.i.d.$라고 가정하고, 영역 $R$ 안에 들어올 확률과 안 들어올 확률에 대해 binomail distribution을 적용할 수 있다.
$$ P(k) = \begin{pmatrix}N \\ K\end{pmatrix} P^k (1-P)^{N-k} $$
그리고 여기서 $k$ 대신 $\frac{k}{N}$을 사용하면 binomail distribution 특성으로 평균과 분산을 구할 수 있다.
$$ E[\frac{k}{N}] = P, \ \ Var[\frac{k}{N}] = \frac{P(1-P)}{N} $$
여기서 만약 $N$이 무한으로 간다고 가정해보자. 분산은 0에 가까워질 것이고, 확률 값은 Montecalro approach로 인해 원하는 영역의 포함되는 data의 개수만큼 근사가 될 것이다.
이를 통해 우리는 아래 식을 얻을 수 있다.
$$ P \cong \frac{k}{N} $$
다음은 $R$이 충분히 작은 영역이라 $p(x)$가 급격하게 바뀌지 않는 다고 가정해보자.
분포식에 존재하는 임의의 점 $x_{1}$과 $x_{2}$에 대해 $p(x_{1}) = p(x_{2})$를 만족하게 되고, 해당 영역은 $p(x_{1}) \times (x_{2} - x_{1})$으로 정의할 수 있다. 이를 통해 확률을 다음과 같이 정의할 수 있다.
$$ P = \int_{R}p(x')dx' \cong p(x)V $$
여기 $V$ 는 volume을 의미하고, 1차원에서 volume은 직선, 2차원은 넓이, 3차원은 부피에 해당한다.
위 2개 식을 merge하면 다음과 같이 식을 정의할 수 있다.
$$ P = \int_{R}p(x')dx' \cong p(x)V = \frac{k}{N}, \ \ p(x) = \frac{k}{NV} $$
이는 영역 $R$에 존재하는 실제 객체 수를 (시행 횟수 * 볼륨)의 식으로 근사할 수 있다.
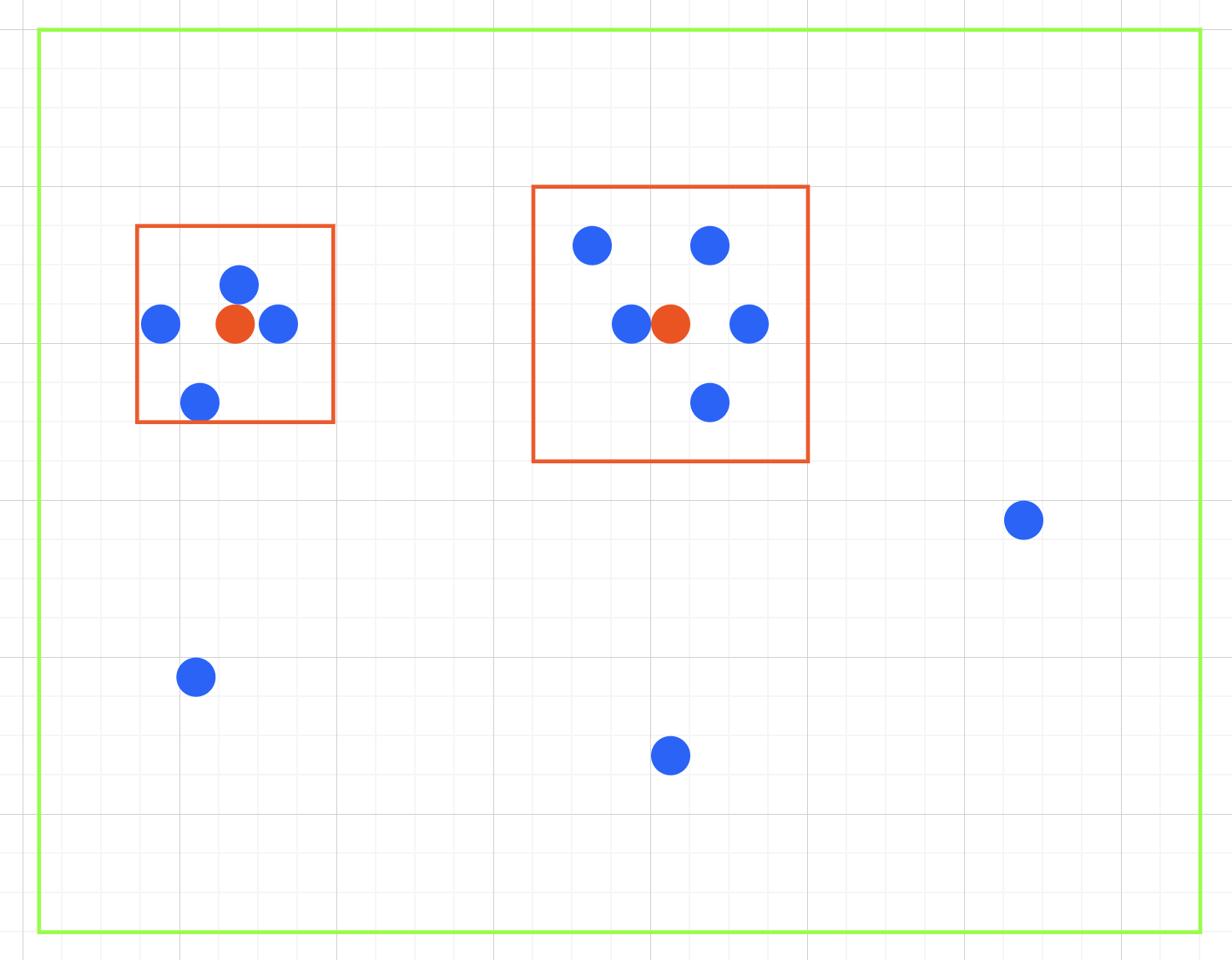
위 식을 시각적으로 이해하기 위해 위와 같은 그림이 있다고 가정하자. 관심 영역 $R$을 빨간색 사각형으로 잡고, 전체 데이터가 총 12개가 존재한다고 하면, 첫 번째 왼쪽 영역의 확률을 $\frac{4}{12\times3^{2}}$로 표현할 수 있다. (사각형 선분의 길이가 3이라고 했을 경우) 두 번째 관심 영역은 $\frac{5}{12*5^{2}}$으로 표현할 수 있다.
여기서 빨간색 점은 영역에 대한 무게 중심이다.
이러한 방법으로 데이터를 통해 분포를 근사하는 것이 kernel density estimation의 목적이다.
$N$ 값이 커질수록, $V$ 값이 작아질수록 estimation의 정확도는 올라간다. 우리는 보통 $N$을 알고 있는 상태로 진행함으로 상수로 두고, $V$에 대한 적절한 값을 조정하는 것을 목표로 하는데, $V$는 이론적으로 2가지 조건을 만족해야 한다.
- $R$안에 많은 sample들을 충분히 넣어야 한다.
- $R$안에 있는 데이터들의 $p$는 constant 해야 한다.
Parzen Window Density Estimation

영역을 정의하기 위해 추정하고자 하는 확률 $p(x)$를 무게 중심 $x$를 가지면서 각 길이가 $h$인 hyper cube를 만든다고 가정하자. 차원을 $d$라고 할 때 hyper cube의 volume은 $V = h^{d}$가 된다.
이를 통해 kernel function $K(u)$를 정의하면 수식은 다음과 같다.
$$ K(u) = \begin{cases} 1 \ |u_{j}|< \frac{1}{2}, \ \ \forall j = 1, \dots,d \\ 0 \ \ \text{otherwise} \end{cases} $$
관심 영역 $R$에 존재하는 데이터의 개수 $k$는 다음과 같은 수식으로 구할 수 있다.
$$ k = \sum_{i=1}^{N}K(\frac{{x}^{i}- {x}}{h}) $$
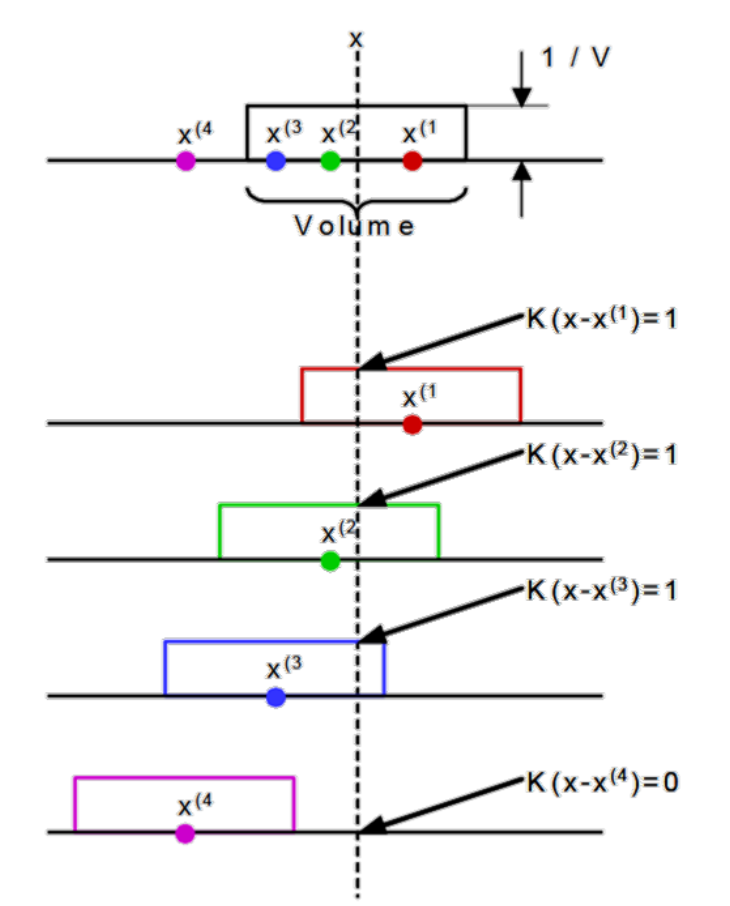
위 수식을 2차원에서 시각화하면 그림과 같다. 여기서 $K$가 의미하는 것은 $x$를 기준으로 관심 영역 안에 들어오는 데이터의 존재를 측정하는 함수가 된다. 위 그림에서 $k$는 3이 된다.
그리고 이를 통해 확률 $p$를 다음과 같이 정의할 수 있다.
$$ p(x) = \frac{1}{Nh^{d}}\sum_{i=1}^{N}K(\frac{{x}^{i}- {x}}{h}) $$
위에서 정의한 $k$와 volume인 $V$를 곱한 값이 $p$가 된다.
이를 통해 $x$를 옮겨가면서 전체에 대한 확률 밀도 함수를 구할 수 있었다. 이것이 바로 Parzen Window Density Estimation의 개념이다. 우리는 이 과정에서 데이터가 어떤 분포를 따른다고 정의를 하지 않고, 관심 영역의 존재하는지에 대한 불연속적인 counting을 진행하였다.

위 그림을 보면 2번째 관심 영역을 보면 노란색 데이터가 2개가 존재한다. 두 데이터의 관심 영역 포함 여부가 다르지만 중심 점으로부터 distance는 그렇게 차이가 나지 않는다.
경계 기준으로 이렇게 값이 달라지는데, 이를 불연속적이라고 하고, 이를 해결하고자 smooth kernel function을 사용한다.

Smooth kernel function은 적분 값이 1인 것을 만족해야 한다. 이를 반대로 말하면 적분 값이 1인 함수들은 모두 smooth kernel function이 될 수 있다는 의미이다.
여기서 가장 기본적으로 도입할 수 있는 함수는 Gaussian이고, 각 데이터의 중심을 gaussian의 중심으로 보고 이에 대해 얼마나 떨어졌는지 개별적으로 확률을 계산한 다음, 전체에 대한 확률 계산을 하는 것이 Parzen window density estimation이다.

다음과 같은 Smooth kernel function들이 존재한다.

Smooth parameter인 h가 크면 오른쪽 아래 그래프와 같이 overshooting을 한다. 반대로 작으면 위 그림들처럼 spiky 하게 된다. 따라서 MLE 등의 method를 통해 h를 결정하는 것이 parzan의 학습 과정이다.

지금까지 설명한 밀도 기반 이상치 탐지의 개념을 다시 보면 왼쪽 Gaussian은 중심이 한 개 존재하고, 타원으로 표현할 수 있다. MOG를 통해 3개의 gaussian을 가지고 estimation을 하면 범위가 조금 더 유연해지고, paran의 경우에는 데이터 각 gaussian을 갖기 때문에 학습이 더욱 잘되는 모습을 볼 수 있다.