[Anomaly Detection] Distance, Clustering, PCA-based Methods
본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다.
1. Distance-based anomaly detection
Distance 기반 anomaly detection은 outlier에 해당하는 객체들은 이웃들과의 거리가 멀 것이라고 가정한다.
이 말은 즉슨 정상 데이터는 근처에 다른 데이터들이 많을 것이라는 것이다.
여기서 핵심은 Normal class에 대해 확률 분포를 가정하지 않는다. 오직 객체 간의 거리만 계산해서 anomaly socre를 측정한다.
KNN based Anomaly Detection을 알아보기 전 KNN에 대해 알아보자.
KNN
traing set에서 주어진 test input $x$와 가장 가까운 $K$개의 point를 본다고 가정하자. KNN은 이때 test input인 $x$가 어떤 class에 속할지를 예측하는 문제이다.
여기서 $K$는 우리가 직접 선택해야 하는 hyperparameter이다.
식은 다음과 같다.
$$p(y = c | x, D, K) = \frac{1}{K} \sum_{i \in N_k (x,D)}{I(y_i = c)}\\
I(e) =
\begin{cases}
1, & \quad if\ e\ is\ true \\
0, & \quad otherwise
\end{cases}$$
$N_{k}(x,D)$는 $x$에 대한 K nearest point의 indices이다.
수식을 해석해보면, $x$가 어느 class에 속하는지 확률적으로 구할 수 있게 된다. 예를 들어 $K=4$인 class의 분포에 대해 어떤 점 $x$에 대한 KNN을 구하게 되면 $\frac{1}{4} \sum_{i \in N_k(x,D)} I(y_i = c)$에서 점 $x$에 대한 4개의 nearest point에 대해 $I(y_i = c)$을 구해 4로 나누면 된다.
정리하면 KNN 알고리즘은 parameter를 학습하는 것이 아니라, 주변 data의 분포를 통해 prediction을 진행하는 것으로 볼 수 있다.
예를 들어 설명하자면 K가 4이고, label은 {사과, 바나나}라고 하자. input data point $x$에 대해 가장 인접한 4개의 data를 비교한다. 만약 가장 인접한 데이터 4개중 3개가 사과, 1개가 바나나라고 하면 위 수식을 통해 사과는 3/4, 바나나는 1/4이기 때문에 최종적으로 input data $x$는 사과라고 판별하게 된다.
KNN classifier의 경우 굉장히 알고리즘적으로 심플하고, 유클라디안이나 L2 distance와 같이 좋은 distance가 주어지면 잘 작동한다.
하지만 KNN의 성능은 feature dimenstion의 증가에 따라 상당히 저하된다. 이러한 문제를 curse of dimensionality라고 부른다.
input data가 D-dimensional 단위로 균일하게 분포되어 있을 때, KNN Classifier를 적용하는 상황을 고려해보자. data point의 원하는 비율 $f$까지 test point $x$ 주변에 hyper-cube를 증가시켜 class label의 density를 추정한다고 가정하자. 그렇다면 기대되는 cube의 edge length 값은 $e_{D} = f^{\frac{1}{D}}$라고 할 수 있다.
만약 $D = 10$이고, density class label의 estimation이 data의 10%에 근거한다면, 기대되는 edge length는 다음과 같다.
$e_{10}(0.1) = 0.1^{0.1} \approx 0.8$
여기서 data의 1%만 사용했다면 식은 다음과 같이 변한다.
$e_{10}(0.01) = 00.1^{0.1} \approx 0.63$
이러한 KNN의 curse of dimensionality를 아래 그림을 통해 다시보자.

왼쪽 그림에서 작은 정육면체인 small cube의 길이를 s라고 하고, large cube를 l이라고 하면 number of dimension의 함수로 unit cube를 커버하는데 필요한 cube의 edge 길이를 오른쪽 그래프처럼 표현할 수 있다
이를 통해 알 수 있는 사실은 feature에 대한 dimension이 커짐에 따라 KNN classifier가 cover 해야 할 data 수가 점점 많아진다. 이는 Nearest neighbor에 대한 data만을 가지고 decision을 하지 못하고, 더욱 넓은 범위의 data를 통해 decision을 해야 함을 의미하며, KNN classifier가 올바르게 동작하지 못하게 된다. 따라서 KNN은 feature dimension이 작은 경우에는 유용하지만, dimension이 큰 경우 model의 complexity가 높아지고, 이에 따라 성능이 낮아진다는 결론을 얻을 수 있다.
KNN (K-Nearest Neighbor) - based Anomaly Detection
Distance 기반 anomaly detection은 outlier에 해당하는 객체들은 이웃들과의 거리가 멀 것이라고 가정한다.
이 말은 즉슨 정상 데이터는 근처에 다른 데이터들이 많을 것이라는 것이다.
여기서 핵심은 Normal class에 대해 확률 분포를 가정하지 않는다. 오직 객체 간의 거리만 계산해서 anomaly socre를 측정한다.
우리는 앞서 Parzen window density estimation에서 $p(x) = \frac{K}{NV}$라는 수식을 살펴보았다.
여기서 $N$ 은 객체의 수, $V$는 영역 $R$에 해당하는 volume, $K$는 해당하는 영역에 존재하는 데이터 수였다.
Parzen window density estimation에서는 $V$를 고정시켰지만, KNN에서는 $K$를 고정시키고 $K$를 커버할 수 있는 $V$를 찾는 개념이다.
$V$를 정의하기 위해 $K$번째 데이터까지의 거리를 어떻게 측정하냐에 따라 결과가 달라지는데, 이에 대한 distance method는 아래와 같다.
1. Maximum distance to the k-th nearest neighbor
$$ d_{max}^{k} = \kappa(\mathbf{x}) = \parallel\mathbf{x} - z_{k}(\mathbf{x}) \parallel$$
2. Average distance to the k-nearest neighbors
$$ d^{k}{avg} = \gamma(\mathbf{x}) = \frac{1}{k}\sum{j=1}^{k}{\parallel \mathbf{x} - z_{j}(\mathbf{x})\parallel} $$
3. Distance to the mean of the k-nearest neighbors
$$ d_{mean}^{k} = \delta(\mathbf{x}) = \parallel \mathbf{x} - \frac{1}{k}\sum_{j = 1}^{k}z_{j}(\mathbf{x}) \parallel $$
여기서 2번은 개별적인 거리를 먼저 계산하고, 이들의 평균 distance를 측정하는 것이고, 3번은 이웃들의 공간 상 무게 중심을 먼저 구한 후, 이를 빼는 방식이다.
위 distance를 통해 anomaly score로 이용할 수 있다.
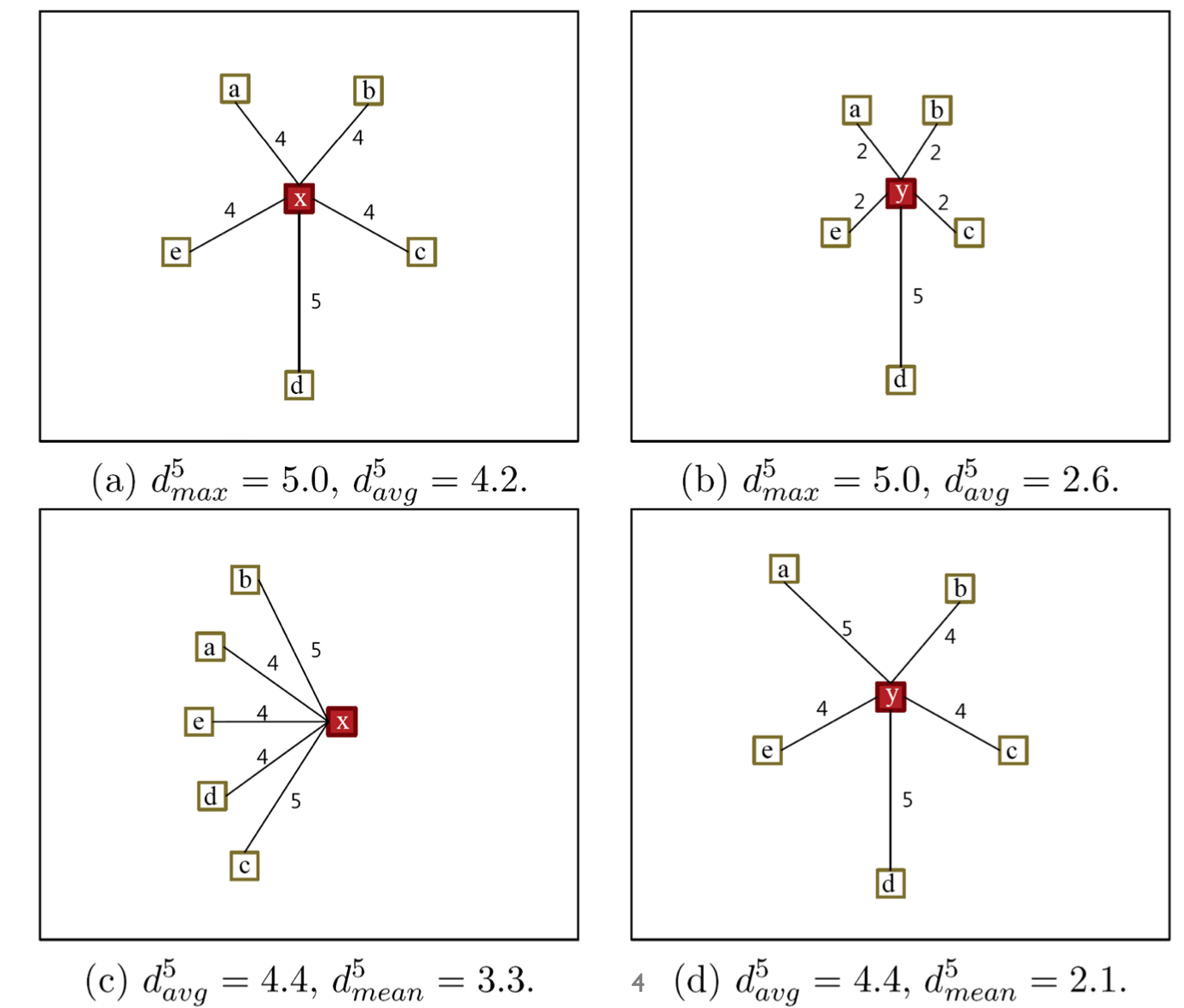
각 distance의 차이를 살펴보면 (a)와 (b)는 $K= 5$일 때 maximum distance는 5.0으로 같지만, avg distance는 다르다. (a)와 (b)의 최대 값은 같지만, 평균값이 다르기 때문이다.
(c), (d)를 보았을 때는 avg distance는 같지만, mean distance는 달라지게 된다. (c)는 이웃들이 한쪽으로 편향되어 있고, (d)는 이웃들이 등방성을 갖기 때문이다.
이를 통해 알 수 있는 사실은 주변 이웃들의 분포에 따라 각 distance가 달라지고, 이에 따라 anomaly score가 달라지는 모습을 볼 수 있다. 각 케이스에 따라 유리한 distance가 달라진다.
2. Clustering-based anomaly dection
Clustering 기반 이상치 탐지에서 대중적인 알고리즘은 DBSCAN이다. 이는 군집화를 하는 과정에서 군집에 속하는 애들이 아니면 이상치라고 판단하는 알고리즘이다.
이 방법 말고도 가까운 군집조차도 멀다고 느껴지면 이상치라고 판단하는 이상치 감지도 존재한다. 대표적으로 K-means clustering-based anomaly detection이 있다.
K-means clustering
K-means clustering은 D 데이터가 주어졌을 때, 각 cluster 내의 중심 점과 각 cluster에 속하는 데이터 D들과의 거리를 최소로 하는 cluster 집합 S를 찾는 과정이다. 여기서 거리는 유클리드 거리, 맨해튼 거리, 해밍 거리를 적용할 수 있고, 보통은 유클리드 거리를 기준으로 진행한다. 또한 집합 S는 총 K개의 cluster의 집합이다.
$$ S_{i}= \{S_{1}, S_{2},\cdots, S_{K}\} $$
위와 같이 K는 cluster의 개수인데, 이는 hyper parameter이므로 사용자가 직접 설정해야 한다. i번째 cluster에 해당하는 중심점을 μ_i라고 정의할 때 K-means clustering의 분산 식은 아래와 같다.
$$ V = \sum_{i=1}^{k}\sum_{D_{i}\in S_{i}}\parallel D_{j} - \mu_{i} \parallel^{2} $$
K-means clustering는 각 cluster 내의 중심 점과 집합 간 거리를 최소화해야 되기 때문에 위 분산 식을 최소화시키는 것이 우리의 목표이다. 목표를 만족하기 위해서는분산을 최소화 시키는 값을 찾아야 한다.
분산 식은 각 cluster 점에 해당하는 와 중심 점에 해당하는 의 유클리드 거리를 의미한다.
K-means clustering은 우선 의 값을 설정해야 한다. 가장 보편적인 초기화 기법인 무작위 분할 기법을 사용하여 를 초기화시킨다.
이후 K-means clustering은 2가지 동작을 반복하며 수렴한다.
- 각 데이터 D에 대한 클러스터 설정
$$ S_{i}^{(t)} = \{D_{p}: \parallel D_{p}- \mu_{i}^{(t)} \parallel^{2} \leq \parallel D_{p} - \mu_{j}^{t} \parallel^{2}, 1 \leq j \leq j \} $$
P번째 데이터 D는 k개의 cluster에 존재하는 중심점과 다른 cluster에 존재하는 의 유클리드 거리를 계산하여 가 작을 경우 해당 데이터를 해당 cluster인 에 할당한다.
- 각 클러스터의 중심 값 재조정
$$ \mu_{i}^{(t+1)} = \frac{1}{\mid S_{i}^{(t)} \mid}\sum_{D_{j} \in S_{i}^{(t)}}D_{j} $$
각 cluster의 중심 값인 μ_i를 구하기 위해 cluster 집합 S_i에 속하는 데이터 셋 D_j들의 합과 cluster 크기와 나누어 무게 중심 값으로 μ_i를 구해 중심 값 재조정을 진행한다.
1, 2번을 무게 중심 값의 변화가 없어질 때까지 반복한 후 최종적인 수렴 값을 얻게 된다. 최종 값들을 통해 K개로 분할된 cluster를 얻을 수 있고, 새로운 데이터가 입력될 시 해당하는 cluster를 통해 분류를 할 수 있다.
K-means clustering-based anomaly detection
위 KMC 개념을 이용하여, 새로운 객체에 대한 anomaly score를 측정한다. 이때 사용하는 distance는 크게 2가지가 존재한다.
1. Absolute distance to the nearest centroid
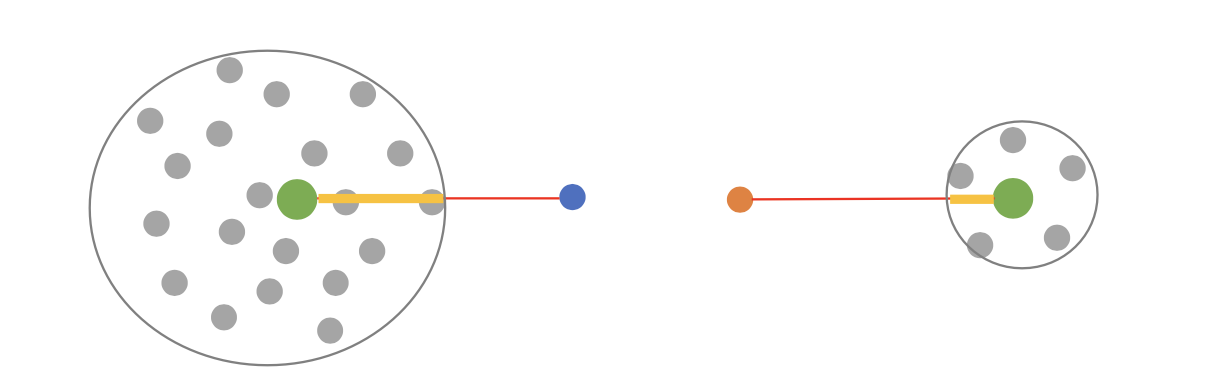
파란색과 주황색에 해당하는 새로운 데이터가 있을 때, 파란색의 경우 가장 가까운 클러스터의 무게 중심인 왼쪽 초록색 (nearest centroid) 부분과의 distance를 구하고, 주황색의 경우 가장 가까운 클러스터의 무게 중신인 오른쪽 초록색 부분과의 distance를 구한다. 이를 통해 anomaly score를 구한다.
2. Relative distance to the nearest centroid
클러스터의 반지름을 계산하여 이와 상대적으로 얼마나 떨어져 있는지를 계산한다.
클러스터의 반지름을 $a_{1}$이라 하고, 클러스터 지름과 데이터의 distance를 $a_{2}$라고 할 때 anomaly score는 $\frac{a_{2}}{a_{1}}$으로 계산한다.
위 그림에 도입을 하면 클러스터의 지름이 작은 주황색이 더 이상치에 가깝다고 판단할 수 있다.
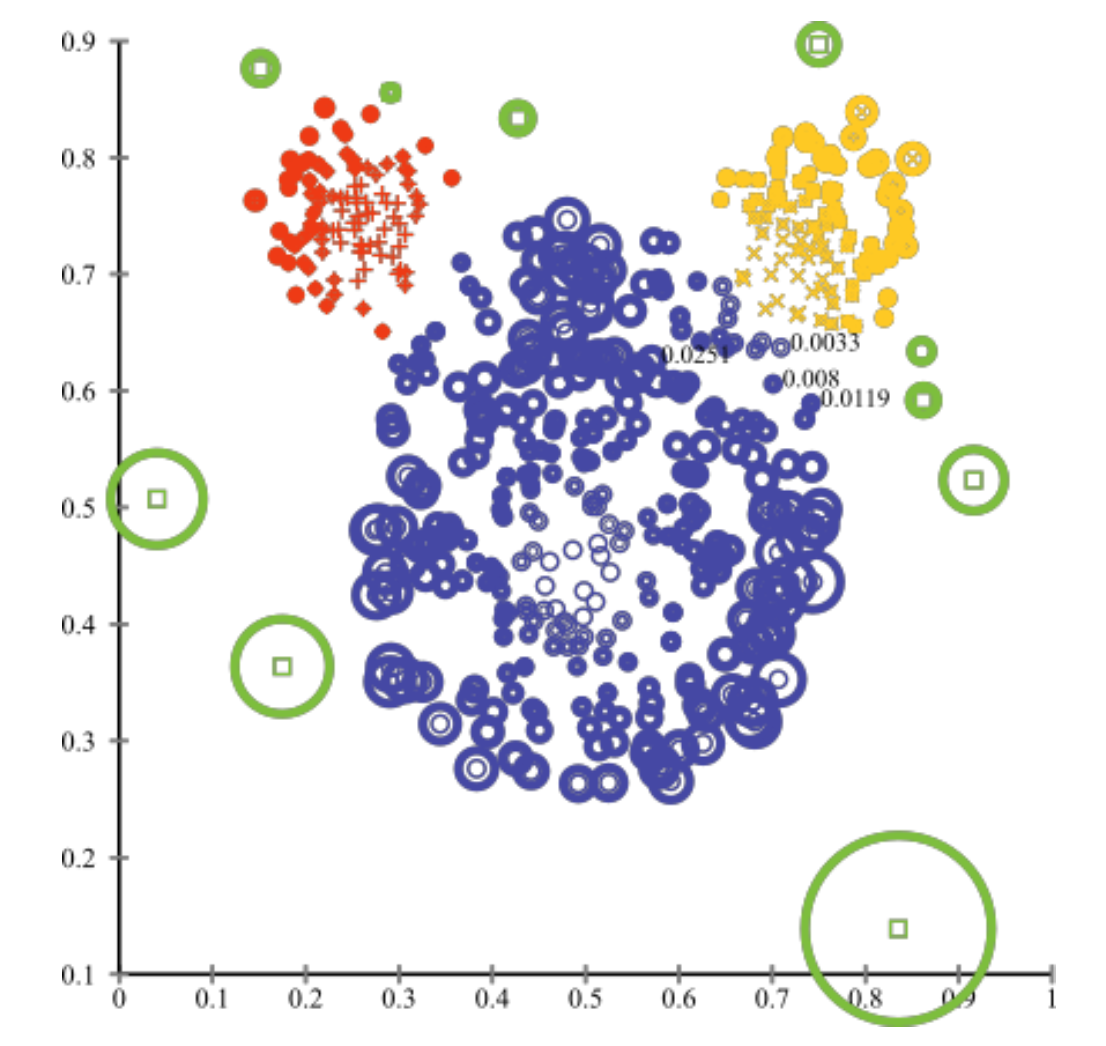
위 plot을 통해 클러스터와 멀어질수록 anomaly score가 더 높아지는 것을 확인할 수 있다.
3. PCA-based anomaly detection
PCA
$$ \max \ \ \mathbf{w}^{T}\mathbf{S}\mathbf{w} \\ s.t. \ \mathbf{w}^{T}\mathbf{w} = 1 $$
PCA는 projection 이후 분산을 최대화하는 $\mathbf{w}$를 찾는 것을 목적으로 한다. 이를 통해 $\mathbf{w}^{T}\mathbf{S}\mathbf{w}$ 를 최적화한다.
이를 위한 objective function은 다음과 같이 정의된다.
$$ L = \mathbf{w}^{T}\mathbf{S}\mathbf{w} - \lambda(\mathbf{w}^{T}\mathbf{w} -1) \\ \frac{\partial L}{\partial \mathbf{w}} = 0 \rightarrow \mathbf{S}\mathbf{w} - \lambda \mathbf{w} = 0 \rightarrow (\mathbf{S}- \lambda \mathbf{I}) \mathbf{w} = 0 $$
해당 MLE의 최적화된 loss를 구하기 위한 최적의 $\mathbf{w}$는 위를 만족해야 하고, 이를 통해 알 수 있는 사실은 $\mathbf{w}$라는 기저는 표준 공분산 행렬의 고유 벡터이고, 이를 통해 보존되는 벡터 값은 고유 벡터이다.
PCA-based anomaly detection
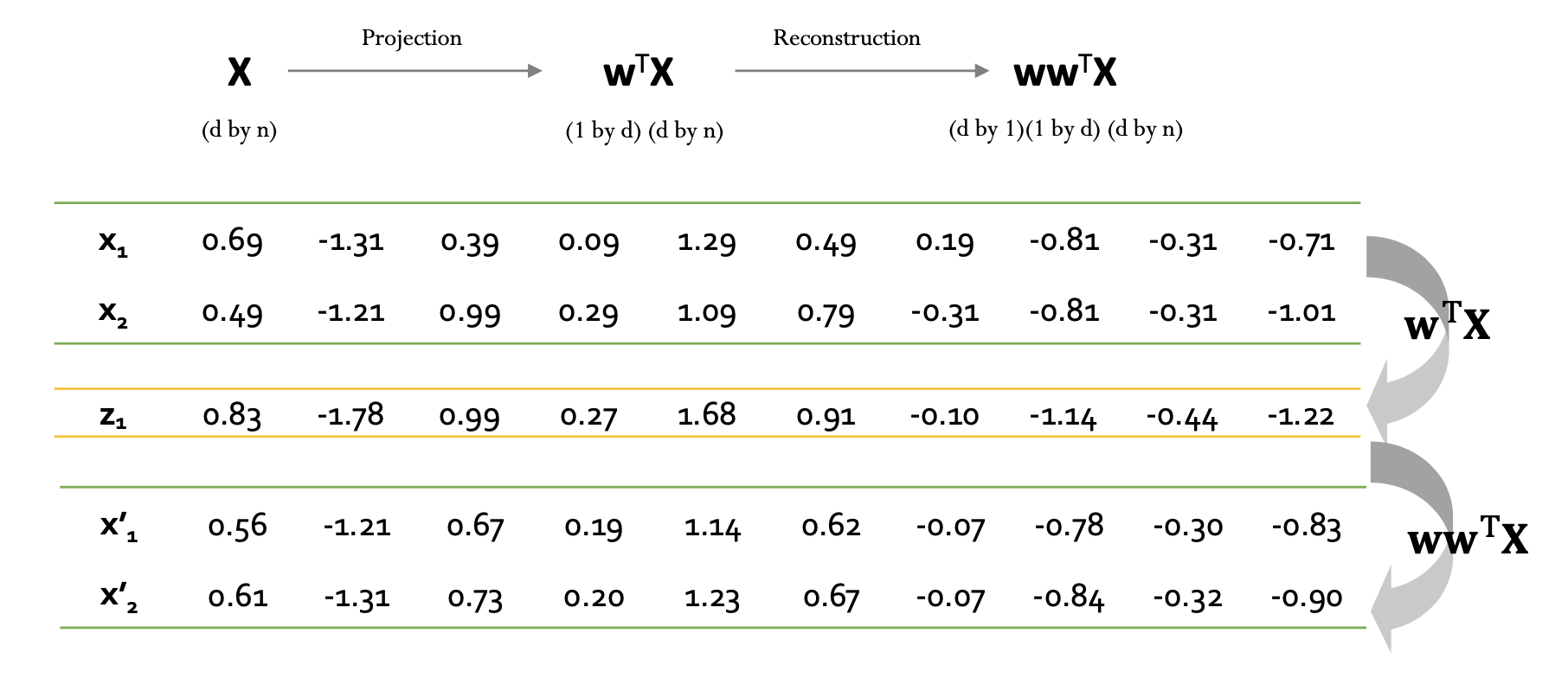
$D \times N$ 크기의 행렬 $X$를 projection 하면 $\mathbf{w}^{T}\mathbf{X}$가 되고, 이를 다시 reconstruction을 진행하면 $D \times N$ 크기의 $\mathbf{w}\mathbf{w}^{T}\mathbf{X}$의 행렬을 얻을 수 있다.
이를 통해 $X$가 만약 정상 데이터라고 하면 projection 전후 값에 대한 차이가 별로 없을 것이고, 비정상의 경우에는 데이터가 비정형적이기 때문에 패턴이 파악되지 않아 차이가 크게 날 것이다.
전 후 값의 차이인 error는 다음과 같이 정의할 수 있다.
$$ \begin{align} error(x) = \parallel \mathbf{x} - \mathbf{w}\mathbf{w}^{T}\mathbf{x} \parallel^{2} = (\mathbf{x} - \mathbf{w}\mathbf{w}^{T}\mathbf{x})^{T}(\mathbf{x} - \mathbf{w}\mathbf{w}^{T}\mathbf{x}) \\ = \mathbf{x}^{T}\mathbf{x} - \mathbf{x}^{T}\mathbf{w}\mathbf{w}^{T}- \mathbf{x}^{T}\mathbf{w}\mathbf{w}^{T}\mathbf{x}+\mathbf{x}^{T}\mathbf{w}\mathbf{w}^{T}\mathbf{w}\mathbf{w}^{T}\mathbf{x} \\ = \mathbf{x}^{T}\mathbf{x}-\mathbf{x}^{T}\mathbf{w}\mathbf{w}^{T}\mathbf{x} = \parallel \mathbf{x} \parallel^{2} - \parallel \mathbf{w}^{T}\mathbf{x} \parallel^{2} \end{align} $$
error에 대한 수식을 전개하면 비교적 간단한 수식으로 변형되고, 기하학적으로 살펴보면 error는 아래와 같게 된다.
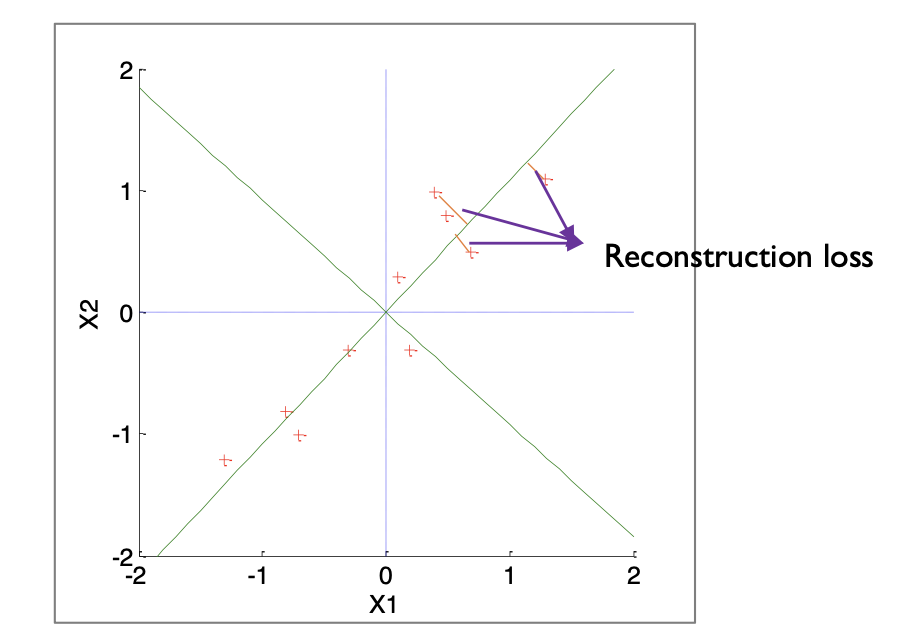
위 plot을 통해 reconstruction loss를 확인할 수 있다.
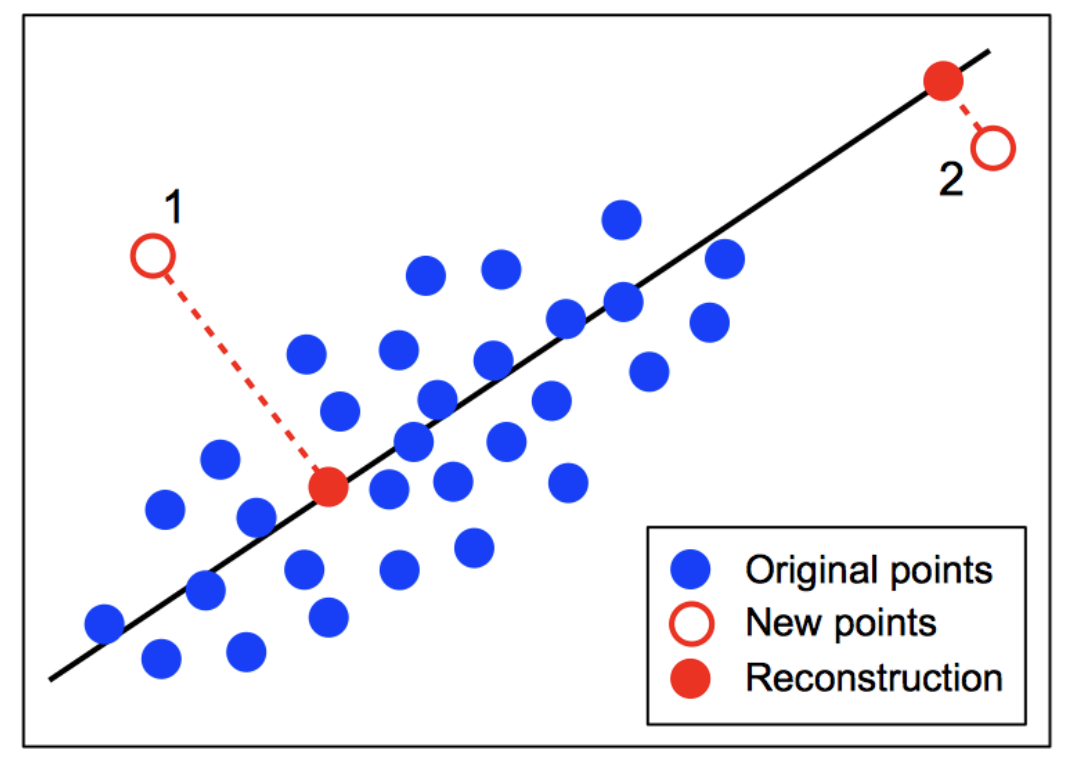
그림을 다시 보면 1번 point의 error는 2번 point 보다 크다. 따라서 anomaly score는 1번이 더 크게 된다.
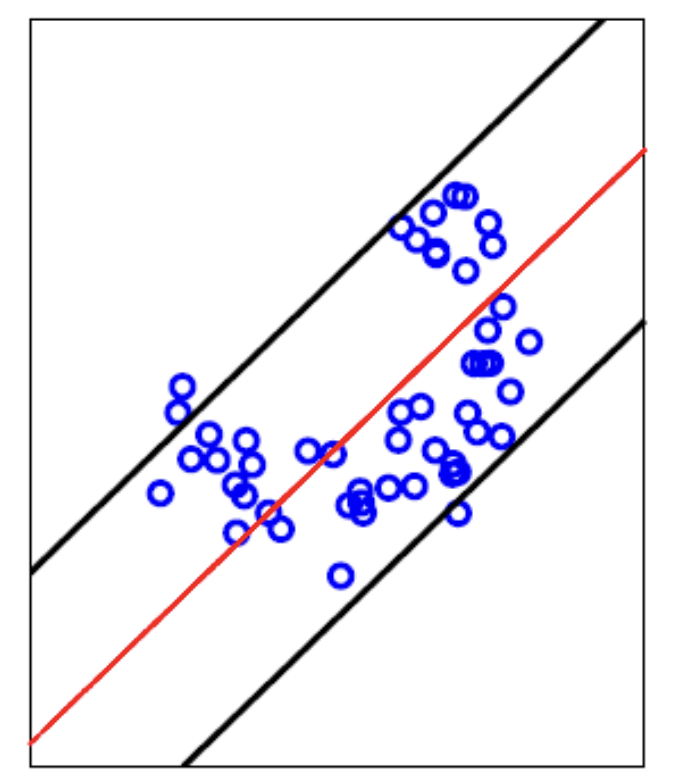
다른 방식으로 살펴보면 빨간 선이 PCA를 통해 구한 주성분이 될 것이고, 이 선을 기준으로 대칭되는 boundary를 정의하면 정상 값에 대한 threshold를 정의할 수 있다.