[Anomaly Detection] Auto-Encoder, One class SVM

본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다.

 

Auto-Encoder for Anomaly Detection

Auto-Encoder 기법은 이미지에서는 CNN을 사용하고, time-series나 text 데이터에 대해서는 RNN 기반으로 사용한다. 이를 모두 관통하는 원칙은 Neural Net을 학습하는 데 있어 input data를 최대한 reconstruction 하여 output data와 비슷하게 만드는 것이다.

$$l(f(\mathbf{x})) = \frac{1}{2}\sum_{k}(\hat{x}_{k}-x_{k})^{2} $$

AE (Auto-Encoder)의 basic loss function은 위와 같이 정의되고, 여기서 $x_{k}$는 input data이고, $\hat{x}_{k}$는 reconstruction 된 output data이다.

Input data $\mathbf{x}$를 축약하여 hidden layer로 보내는 역할을 encoder라고 하고, 여기서 핵심은 hidden layer가 $h$차원이라고 하고, input data가 $d$차원이라면 $h$는 무조건 $d$보다 작아햐 한다. 무조건 정보의 축약 또는 압축이 일어나야 한다는 뜻이다.

이렇게 압축된 데이터를 원래의 차원으로 펼치는 과정을 decoder가 한다.

이 과정에서 $h$ 차원으로 축약된 벡터를 latent vector라고 한다.

위에서 정의한 loss function을 가지고 anomaly score로 사용할 수 있다.

$32^{2}$ 차원을 가진 벡터 이미지를 예로 들어 AE를 시각화하면 위 그림과 같아진다.

Support Vector-based Anomaly Detection

SVM (Support Vector Machine)은 binary classification을 위한 알고리즘이고, SV regression은 회귀 모형 알고리즘이다. 이 알고리즘을 기반으로 anomaly detection에 접근할 수 있다.

이전에 배웠던 밀도 기반 방법론을 통해 특정 데이터가 들어왔을 때 정상 범주에 들어올 확률 및 anomaly score를 냈는데, SV based anomaly detection은 정상과 이상치 데이터에 대한 범주를 찾는다. 이를 찾기 위한 방식이 2가지 있는데 1-SVM (One-class SVM), SVDD이다.

이 알고리즘의 차이는 hyper plane을 구하는 것과 hyper sphere를 구하는 것으로 크게 나뉜다.

이를 자세하게 살펴보자.

One-class Support Vector Machine (1-SVM)

1-SVM은 original data를 feature space로 옮기는데, 이때 정상 데이터를 최대한 원점에서 멀어지도록 만든다. 그래서 원점으로부터 해당 데이터까지의 거리를 $\rho$ 라는 hyper parameter를 가지고 온다.

아래 식을 통해 최적화에 대한 objective function을 살펴보자.

$$ \min_{\mathbf{w}}{\frac{1}{2} \parallel \mathbf{w} \parallel^{2} + \frac{1}{\nu l} \sum^{l}_{i = 1} {\xi}_{i} - \rho} \\
s.t. \ \ \mathbf{w} \cdot \Phi(\mathbf{x_{i}})  \geq \rho - \xi_{i} \\
i = 1,2, \cdots, l\ \  , \xi_{i} \geq0$$

Objective function의 첫 번째 term은 $\mathbf{w}$에 대해 regularization을 진행한다. 이를 통해 $\mathbf{w}$를 최소화한다.

두 번째 term은 개별적인 normal object가 $\rho$ 보다 가까울 때 패널티를페널티를 준다. 즉 정상 영역의 데이터는 원점보다 바깥쪽에 있어야 하는데 그러지 않을 때 페널티를 주는 역할을 한다.

세 번째 term인 $\rho$는 원점에서부터 최대한 멀리 떨어진 hyper plane과의 거리를 의미 한다.

이를 통해 1 term은 model의 변동성을 감소시키고, 2 term은 경계면 조건을 만족하지 못하는 정상 데이터에 대한 페널티를 부여하고, 3 term은 decision boundary를 예측한다.

이를 primal Lagrangian problem으로 변형시키자.

$$L = \frac{1}{2} \parallel \mathbf{w} \parallel^{2} + \frac{1}{\nu l} \sum^{l}_{i = 1} {\xi}_{i} - \rho - \sum^{l}_{i=1}\alpha_{i}(\mathbf{w} \cdot \Phi(\mathbf{x_{i}}) - \rho +\xi_{i}) - \sum_{i=1}^{l}\beta_{i}\xi_{i} $$

원래 objective function에 새로운 term을 추가하였다.

4 term은 개별적인 객체는 원점보다 멀리 있어야 하고, 그렇지 않으면 페널티를 부여하는 역할을 한다.

5 term은 $\xi_{i}$는 항상 0보다 커야 하니깐 이것에 대한 제약식, 즉 페널티를 의미한다.

이를 통해 각 $\mathbf{w}, \xi, \rho$에 대한 KKT condition을 구해보자.

$$\begin{align*} &\frac{\partial L}{\partial \mathbf{w}} = \mathbf{w} - \sum^{l}_{i = 1}{\alpha_{i}\Phi(\mathbf{x}_{i})} = 0 \rightarrow \mathbf{w} = \sum^{l}_{i=1}\alpha_{i}\Phi(\mathbf{x}_{i}) \\
&\frac{\partial L}{\partial \xi_{i}} = \frac{1}{\nu l} -\alpha_{i} - \beta_{i} = 0 \rightarrow \alpha_{i} = \frac{1}{\nu l} - \beta_{i} \\
&\frac{\partial L}{\partial \rho} = -1 + \sum^{l}_{i=1}{\alpha_{i} = 0}\rightarrow \sum^{l}_{i=1}\alpha_{i} = 1
\end{align*} $$

각 parameter에 대한 편미분을 진행하면 위와 같은 식이 도출된다.

$\xi$에 대해 편미분을 진행하면 $\alpha$에 대한 식으로 전개할 수 있고, $\rho$에 대한 미분을 진행하면 $\alpha$에 대한 sum이 1이 되어야 된다는 식이 만들어진다.

이렇게 구한 식으로 primal Lagrangian 식에 대입하면 Dual Lagrangian problem으로 풀 수 있다.

$$L = \frac{1}{2}\sum_{i=1}^{l}\sum^{l}_{j=1}{\alpha_{i}\alpha_{j}\Phi(\mathbf{x}_{i})\Phi(\mathbf{x}_{j})}+\frac{1}{\nu l}\sum^{l}_{i=1}\xi_{i} - \rho \\
-\sum_{i=1}^{l}\sum^{l}_{j=1}{\alpha_{i}\alpha_{j}\Phi(\mathbf{x}_{i})\Phi(\mathbf{x}_{j})} + \rho \sum^{l}_{i=1}\alpha_{i} - \sum^{l}_{i=1}\alpha_{i}\xi_{i} - \sum^{l}_{i=1}\beta_{i}\xi_{i}$$

 

위 수식에 KKT condition에서 구한 수식을 삽입하면 다음과 같이 정리가 된다. (최소화로 변경)

$$ \min L = \frac{1}{2}\sum_{i=1}^{l}\sum_{j=1}^{l}\alpha_{i}\alpha_{j}\Phi(\mathbf{x}_{i})\Phi(\mathbf{x}_{j}) \\
s.t. \ \sum^{l}_{i=1}\alpha_{i} = 1, \ 0 \leq \alpha_{i} \leq \frac{1}{\nu l}$$

이를 통해 $\alpha$에 대한 깔끔한 convex 함수로 만들 수 있다.

식을 더욱 간편화 하기 위해 $\Phi$에 대한 수식을 kernel function으로 바꿀 수 있다.

$$\min L = \frac{1}{2}\sum_{i=1}^{l}\sum_{j=1}^{l}\alpha_{i}\alpha_{j}K(\mathbf{x}_{i},\mathbf{x}_{j})\\
s.t. \ \sum^{l}_{i=1}\alpha_{i} = 1, \ 0 \leq \alpha_{i} \leq \frac{1}{\nu l}$$

$\alpha$의 의미에 대해 알아보자. $\alpha$에 대한 조건은 다음과 같다.

$$ \sum^{l}_{i=1}\alpha_{i} = 1, \ 0 \leq \alpha_{i} \leq \frac{1}{\nu l},\\
  \ \beta_{i}\xi_{i} = 0,\ \alpha_{i} + \beta_{i} = \frac{1}{\nu l} $$

$\alpha$의 값에 따라 위치가 달라진다.

 

Case 1 : $\alpha_{i}=0$ → a non-support vector

여기서 $\alpha_{i}=0$라는 의미는 $\beta_{i}$가 0이 아니라는 것이고, 이는 조건에 의해 $\xi_{i} = 0$이라는 것과 같다. 결국 이 객체들은 SV가 아닌 hyper plane으로부터 멀리 떨어진 객체들을 의미한다.

Case 2 : $\alpha_{i} = \frac{1}{\nu l}$ → $\beta_{i} = 0$ → $\xi_{i} > 0$ → Support vector

해당 케이스를 만족하려면 $\beta$는 0이 되어야 하고, $\xi$는 0보다 커야 한다.

이를 만족하는 $\alpha$는 support vector가 되고, hyper plane 안쪽 원점과 가까운 부분에 위치하게 된다.

Case 3 : $0 < \alpha_{i} <\frac{1}{\nu l}$ → $\beta_{i} > 0$ → $\xi = 0$ → Support vector

해당 부등식을 만족하는 $\alpha$는 결국 $\xi$가 0이 되고, 이는 support vector 이면서 hyper plane 위에 위치하게 된다.

위 3가지 경우를 plot화 하면 다음과 같이 표현할 수 있다.

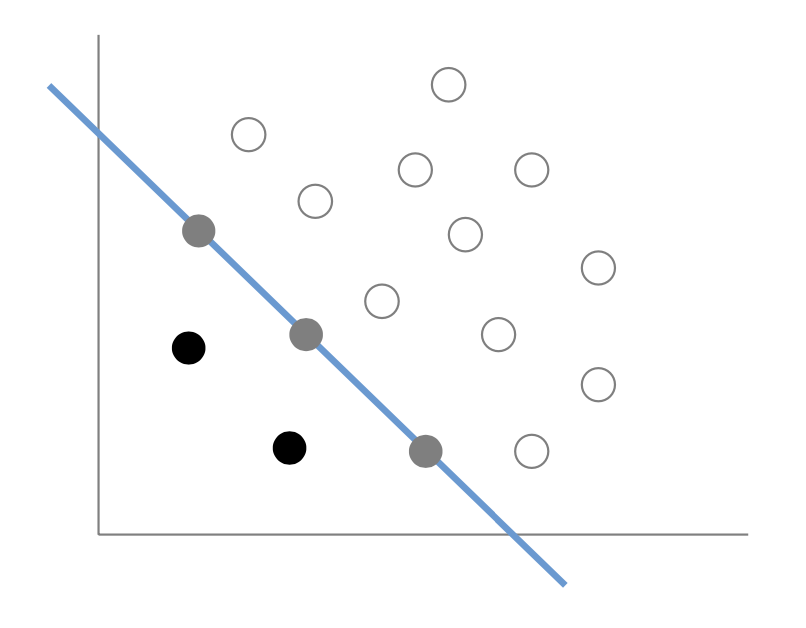
case 1은 하얀색, case 2는 검은색, case 3은 회색으로 표현할 수 있다.

이번에는 $\nu$의 역할에 대해 알아보자.

$0 \leq \alpha_{i} \leq \frac{1}{\nu l}$ 를 만족할 때 $\alpha$의 합은 1이 되어야 한다. 이는 $\alpha$가 가질 수 있는 최대 값인 $\frac{1}{\nu l}$일 때, sum이 1이 되려면 $\alpha$는 $\nu l$개가 된다. 이는 결국 우리는 최소한 $\nu l$ 만큼 support vector가 있어야 한다.

그리고 이때 $\beta_{i}= 0$이 된다. 이때 $\xi_{i} >0$ 이 되고, 이는 hyper plane을 만들었을 때 원점에 더 가까운 SV가 $\frac{1}{\nu l}$이라는 Lagrangian multiply 값을 가졌는데, 그러면 이 hyper plane을 넘어가는 최대의 객체 수가 $\frac{1}{\nu l}$이 된다는 의미이다.

이 말이 조금 어려운데, 예를 들어 $\alpha$가 200개 있다고 하자. 이는 sv의 수가 200개라는 의미이고, 이 경우에는 원점에 더 가까운 $\xi$ 보다 큰 sv는 없다는 의미이다. 따라서 $\nu l$이라는 것은 우리가 가질 수 있는 sv의 최소 개수이고, 동시에 페널티를 줄 수 있는 객체의 최대 값을 의미한다.

결과론 적으로 $\nu$는 sv 비율의 lower boundary면서 $\xi$라는 페널티에 영향을 받을 수 있는 upper boundary이다.

만약 $\nu$가 0.1이면 10% 이상은 sv라는 것이고, hyper plane을 벗어나는 페널티를 부여받는 sv의 최대 비율이 10%이다.

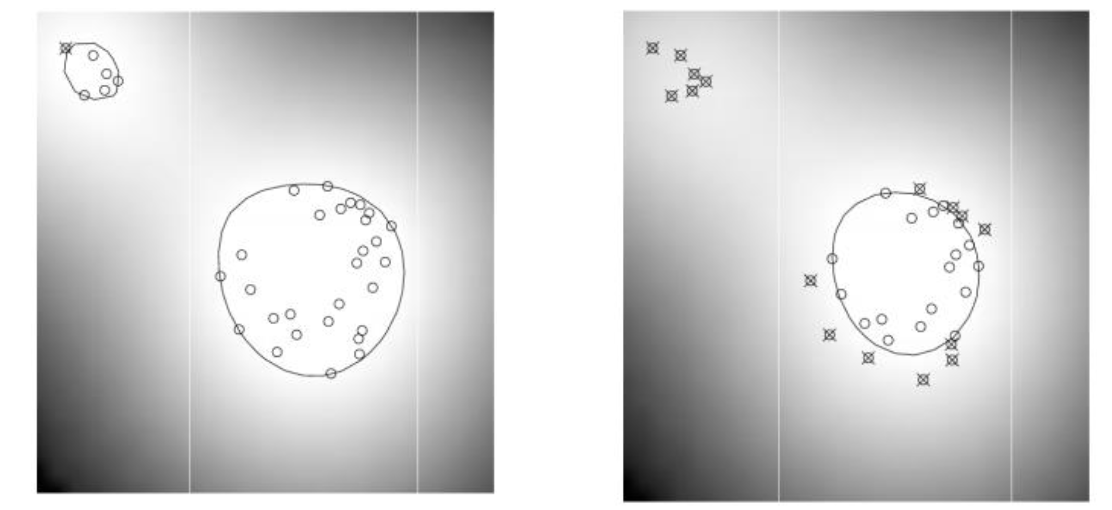
따라서 0.1 일 때와 0.9일 때를 구별해보면 sv가 많을수록 오른쪽과 같이 specialization에 집중하게 된다.

이를 통해 $\nu$의 값에 따라 결과물에 대한 형태를 추정할 수 있게 된다.