[Dimensionality Reduction] Supervised Methods 1: Forward selection, Backward elimination, Stepwise selection

본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다.

 

Feature selection

Feature selection은 가지고 있는 변수 중 의미 있는 일부분의 변수를 추출하는 것이다. 원본의 변수를 치환 또는 변환을 하지 않는다.

Exhaustive Search

가장 쉽게 생각할 수 있는 feature selection 기법은 exhaustive search가 있다. 이는 가능한 모든 조합에 대해 탐색을 하여 feature selection을 진행하는 방법이다.

$$ x_{1}, x_{2},x_{3} $$

만약 위와 같이 3개의 변수가 있다면, 이에 해당하는 모든 조합은 아래와 같이 총 7가지가 된다.

$$ (x_{1}), (x_{2}),(x_{3}),(x_{1},x_{2}), (x_{1},x_{3}),(x_{2},x_{3}), (x_{1},x_{2}, x_{3}) $$

해당 변수에 대해 AIC, BIC, Adjusted $R^{2}$와 같은 지표를 사용하여 성능이 가장 좋은 변수의 조합을 선택하면 된다.

Exhaustive search는 변수의 개수가 많아지면 모델에 대한 연산 시간이 매우 많이 걸리게 된다. 위 plot에서 초록색 그래프가 exhaustive search의 연산 속도이다. exhaustive search의 장점은 global opimal을 찾을 수 있다는 점이다.

Forward Selection

Exhaustive search보다는 성능은 좋지 않지만, 시간을 줄이는 방법으로는 Forward selection과 Backward elimination이 있다.

FS (Forward Selection)부터 살펴보자. 아래와 같이 linear regression model을 기준으로 보자.

총 8개의 변수가 존재할 때 FS는 우선 각 변수를 1개씩만 사용한다. 각 조합에 대한 $R^{2}$를 지표를 사용한다고 가정하자.

위 수식에서는 $x_{2}$를 사용할때가 가장 성능이 높은 것을 확인할 수 있다.

$x_{2}$를 고정하고, 다시 8개의 변수를 각각 더한다. 여기에 대해서도 $R^{2}$를 적용한다. $x_{7}$이 가장 높은 것을 볼 수 있다.

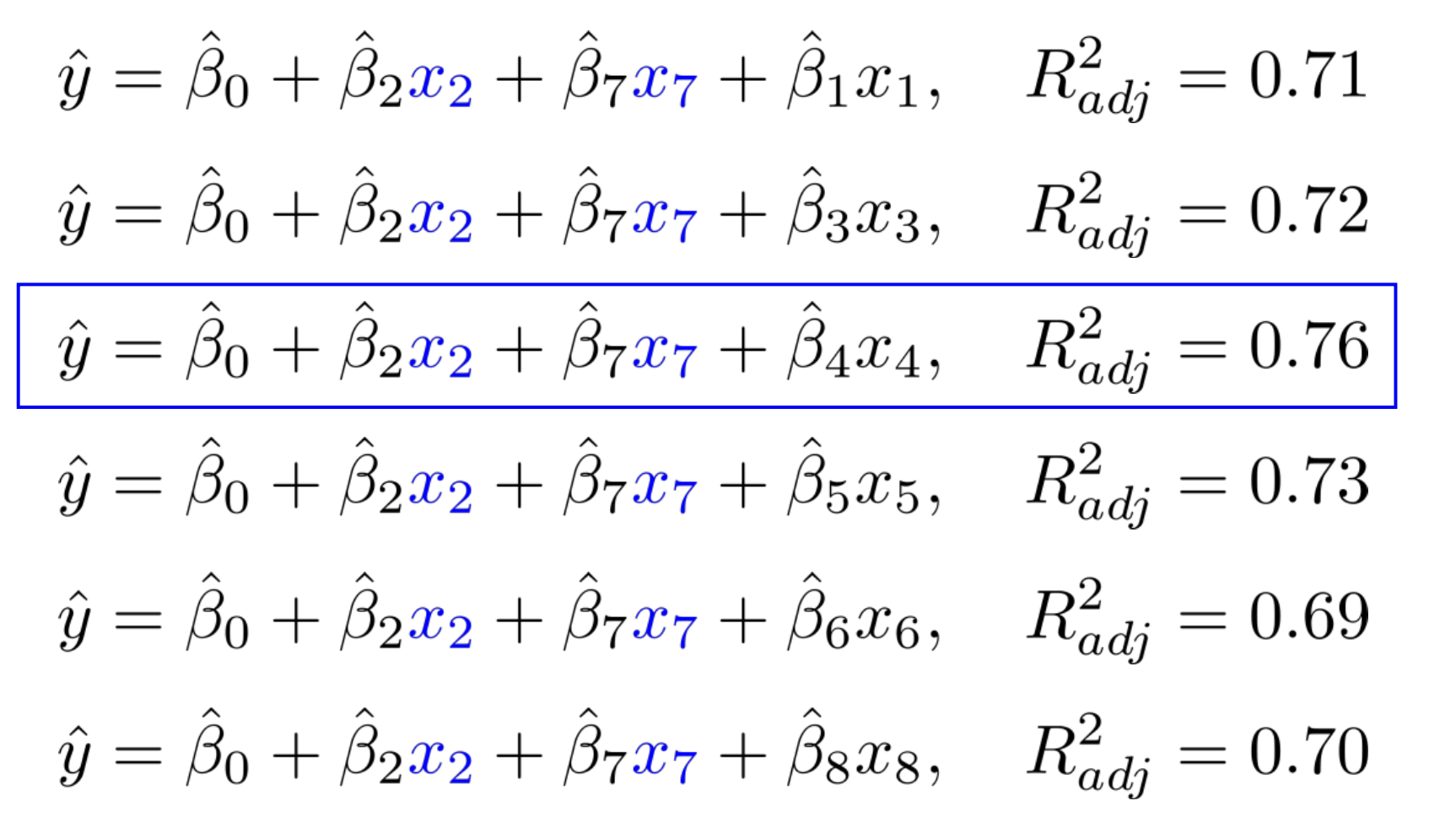
$x_{7}$를 고정한 후 다시 반복한다. $x_{4}$를 채택한다.

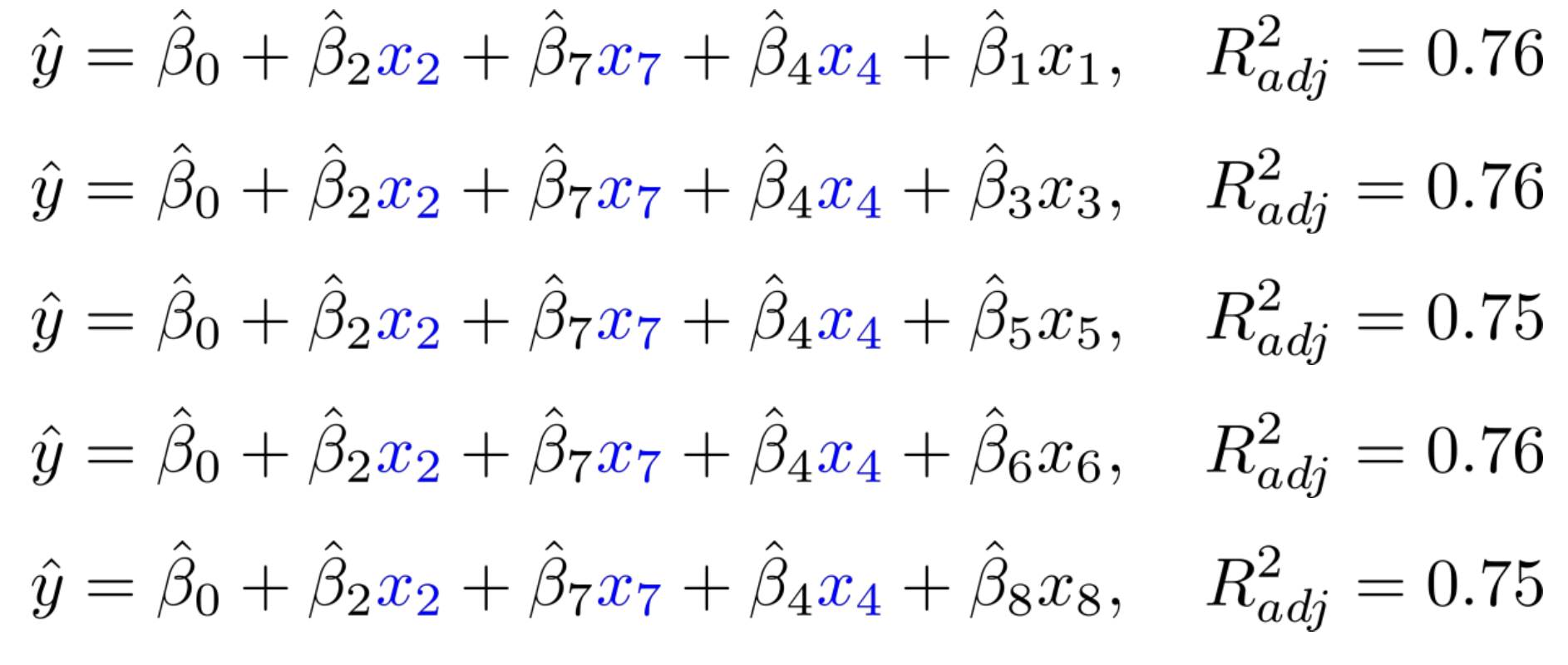
$x_{4}$까지 고정한 후 지표를 측정해보면 더 이상 $R^{2}$가 증가하지 않는 모습을 볼 수 있다. 최종적으로 우리는 FS를 통해 아래와 같은 model을 선택한다.

$$ \hat{y} = \hat{\beta_{0}} + \hat{\beta_{2}}x_{2}+ \hat{\beta_{7}}x_{7}+ \hat{\beta_{4}}x_{4}, \ \ R^{2}_{adj}=0.76 $$

FS는 추가 된 변수에 대해 절대로 제거가 되지 않는다는 특징을 가지고 있다.

Backward Elimination

BE (Backward Elimination)는 FS의 반대라고 생각하면 된다. 쉽게 말해 변수를 하나씩 없애는 방법론이다.

$$ \hat{y} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{1}+ \hat{\beta_{2}}x_{2}+\hat{\beta_{3}}x_{3}+\hat{\beta_{4}}x_{4}+\hat{\beta_{5}}x_{5}+\hat{\beta_{6}}x_{6}+\hat{\beta_{7}}x_{7}+\hat{\beta_{8}}x_{8}, R^{2}_{adj}=0.77 $$

위와 같이 linear regression model이 있다고 하자.

여기서 각 변수를 하나씩 뺀 후 이에 대한 지표를 측정한다. 결과에 대한 감소 값을 hyper parameter로 두고, 해당 값보다 낮아지면 BE를 종료한다.

위 결과를 보면 $x_{3}$을 제거 하였을 때가 가장 성능이 좋은 것으로 보인다.

그 후 다시 하나씩 제거 한다. $x_{8}$을 제거하였을 때 가장 작게 감소한 모습을 볼 수 있다.

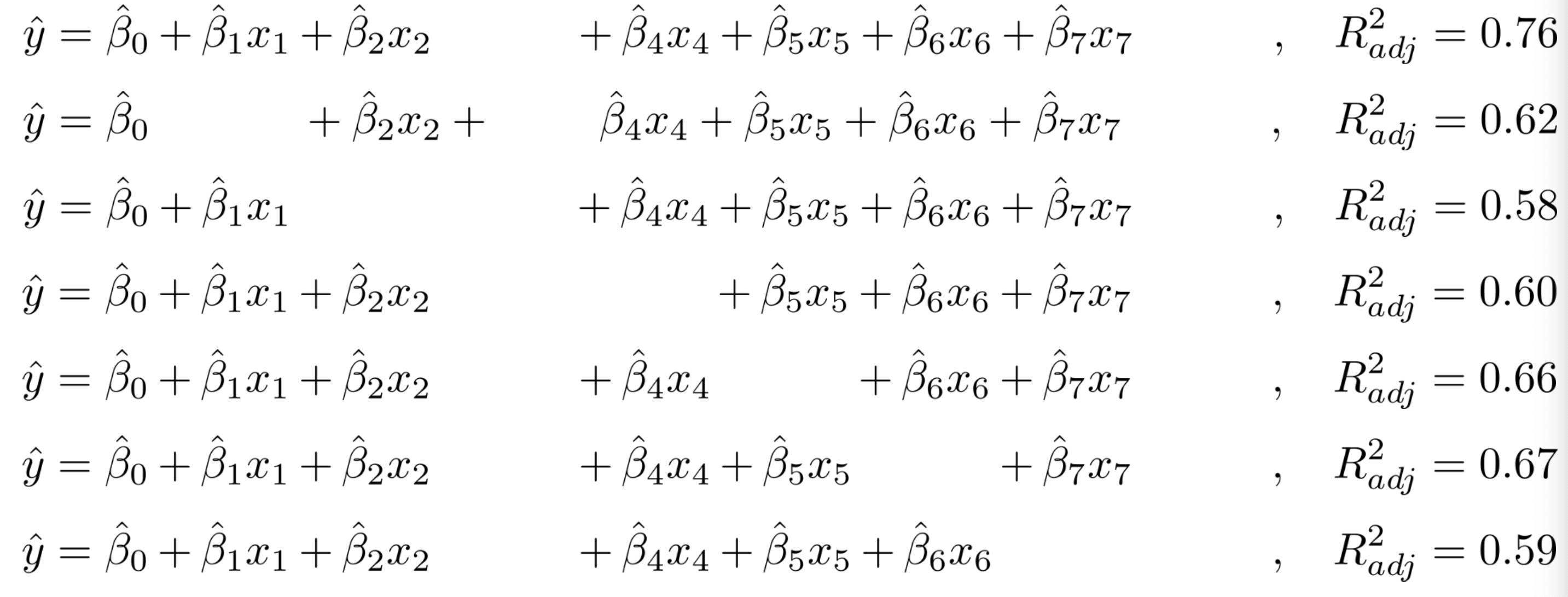
이 후 지표에 대한 감소가 커짐과 동시에 BE를 종료한다. 최종적으로 아래 수식과 같은 모델을 채택한다.

$$ \hat{y} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{1}+ \hat{\beta_{2}}x_{2}+ \hat{\beta_{4}}x_{4}+\hat{\beta_{5}}x_{5}+\hat{\beta_{6}}x_{6}+\hat{\beta_{7}}x_{7}+, \ \ R^{2}_{adj}=0.76 $$

BE의 경우는 FS와는 다르게 한번 제거된 변수는 절대로 추가가 되지 않는다.

Stepwise Selection

FS, BE 보다 연산량은 많지만, 성능을 더 좋게하기 위해 stepwise selection이라는 방법론이 등장했다. 이는 FS와 BE를 번갈아가면서 수행한다. 이로 인해 변수가 선택이나 제거되어도 다음 텀에서 다시 제거되거나 선택될 수 있다.

$$ \hat{y} = \hat{\beta_{0}} + \hat{\beta_{2}}x_{2}, \ \ R^{2}_{adj}=0.56 $$

우선은 FS를 통해 성능이 가장 높은 변수를 선택한다. 위 수식을 통해 $x_{2}$를 선택한 모습을 볼 수 있다.

이후 제거를 해야 하지만, 초기 값보다는 $x_{2}$를 선택한 것이 성능이 더 좋아 제거하지 않는다.

그 후 다시 FS를 진행한다.

$$ \hat{y} = \hat{\beta_{0}} + \hat{\beta_{2}}x_{2}+ \hat{\beta_{7}}x_{7}, \ \ R^{2}_{adj}=0.70 $$

FS를 통해 $x_{7}$을 선택한 모습을 볼 수 있다.

그 다음 제거를 해야 하지만, $x_{2}, x_{7}$을 제거해도 성능이 좋아지지는 않아 그대로 내버려둔다.

$$ \hat{y} = \hat{\beta_{0}} + \hat{\beta_{2}}x_{2}+ \hat{\beta_{7}}x_{7} + \hat{\beta_{4}}x_{4}, \ \ R^{2}_{adj}=0.76 $$

FS를 통해 $x_{4}$를 선택하였다.

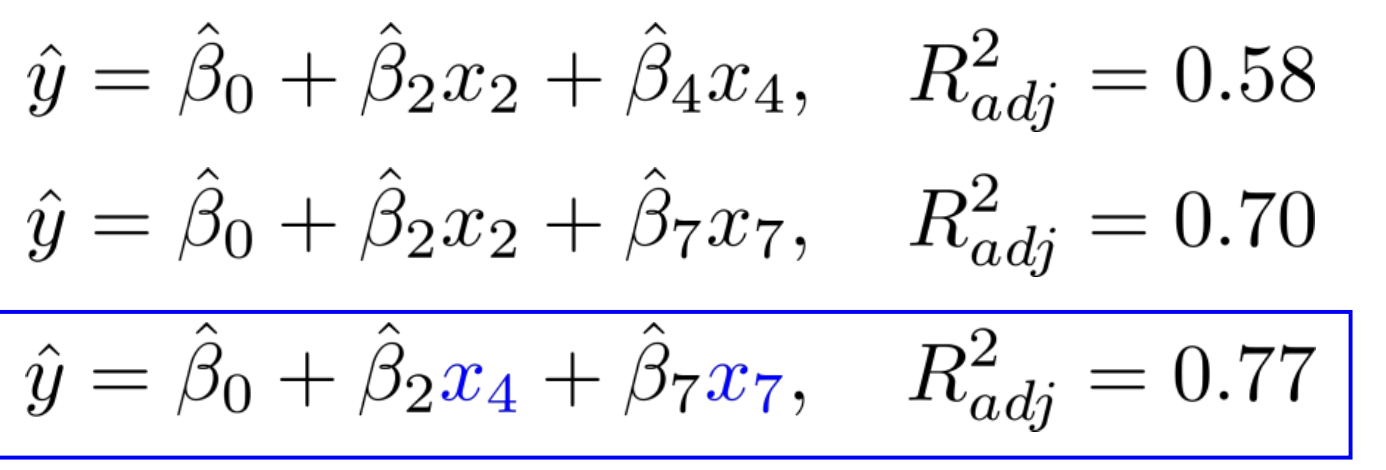
이후 BE를 진행하였는데, $x_{2}$를 제거했는데 성능이 더 좋아진 모습을 볼 수 있다. 따라서 $x_{2}$를 제거한다.

이후 다시 FS, BE를 반복한 후, 성능이 개선이 되지 않을 때까지 반복한다.