[Dimensionality Reduction] Unsupervised Method (Linear embedding) 1: Principal component analysis (PCA)

본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다.

 

차원 축소의 목적은 특정한 머신 러닝 모델을 만들기 위해 특성을 보존하면서 compact 한 데이터를 유지하는 것이다.

이전 챕터까지는 변수 선택에 대해 알아보았고, 이번 챕터부터는 변수 추출에 대해 알아보자.

변수 추출의 목적은 데이터의 속성을 최대한 보존하는 방향으로 새로운 변수들을 생성하는 것이다. 주성분 분석의 목적은 서로 직교하는 기저를 찾는 것이다. 즉, 원 데이터의 분산을 최대한 보존하는 기저를 찾는 것에 초점을 잡는다. 주성분 분석을 하면 원 데이터보다 차원은 무조건 작아져야 한다.

위 그림과 같이 만약 데이터가 있고, PC (Principal Component)가 2개라고 할 때, 우리는 분산이 더 큰 PC를 더 선호해야 한다. 따라서 오른쪽이 더 선호도가 높다고 할 수 있다.

PC를 선택하기 위해 우리는 분산 보존량을 계산할 수 있다. 뒤에서 자세히 살펴보겠지만 $\lambda$가 분산 보존량을 의미한다.

본격적으로 PCA 과정에 대해 살펴보자.

 

Step 1. Data Centering

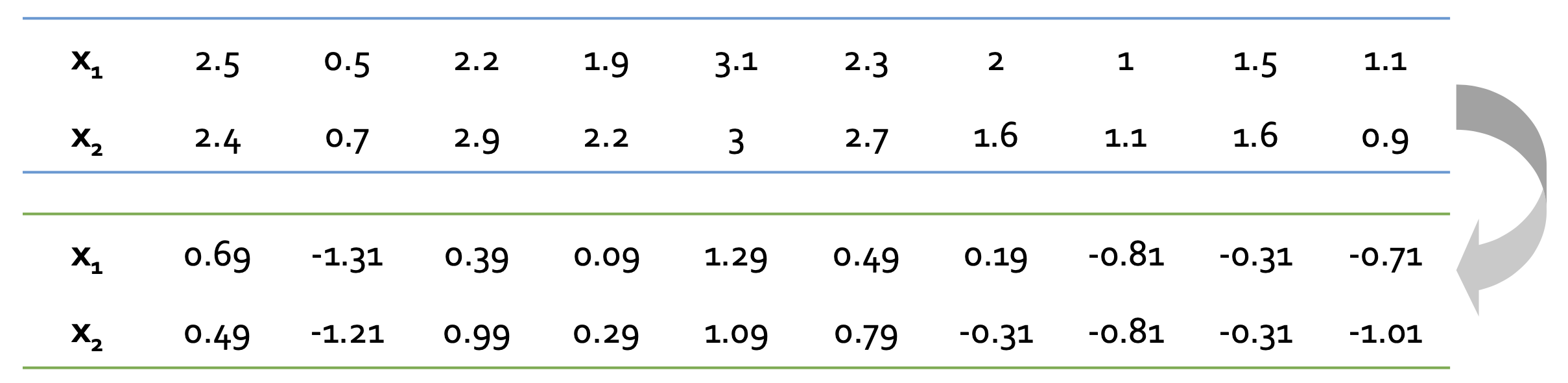
데이터 센터링을 위해 각 데이터들의 평균을 0으로 맞춘다. 추후 계산식의 $x-\bar{x}$ 과정을 간략화하기 위해 진행한다.

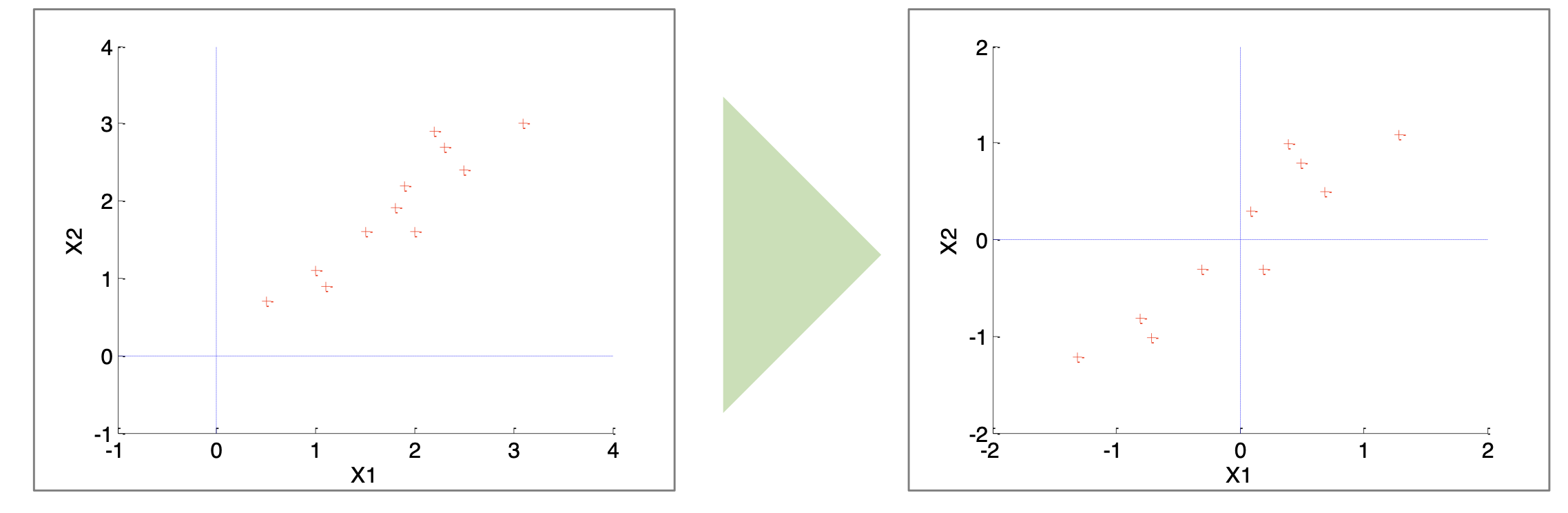
오른쪽 plot이 데이터 센터링에 대한 결과이다.

Step 2. Formulate the optimization problem

Optimization 수식은 다음과 같다. 벡터 $\mathbf{X}$가 bias $\mathbf{w}$에 projection 되었을 때 variance는 아래 식과 같이 정의된다.

$$ V = \frac{1}{n}(\mathbf{w}^{T}\mathbf{X})(\mathbf{w}^{T}\mathbf{X})^{T} = \frac{1}{n}\mathbf{w}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{w}=\mathbf{w}^{T}\mathbf{S}\mathbf{w} $$

$\mathbf{S}$는 normalize 된 $\mathbf{X}$의 sample covariance이다.

우리는 위 수식에서 맨 오른쪽 수식을 최대화시켜야 한다. (분산을 최대로 보존해야 되기 때문에)

Step 3. Obtain the solution

$$ \max \ \mathbf{w}^{T}\mathbf{S}\mathbf{w} \\ s.t. \mathbf{w}^{T}\mathbf{w} = 1 $$

위 정의와 같이 우리는 분산 식을 최대화 해야 한다. 이 식에 라그랑주 재약식을 통해 아래와 같은 수식으로 정리할 수 있다.

$$ L = \mathbf{w}^{T}\mathbf{S}\mathbf{w}-\lambda(\mathbf{w}^{T}\mathbf{w}-1) $$

해당 식에 $\mathbf{w}$에 대한 편미분을 진행하면 최적의 값을 찾을 수 있다.

$$ \frac{\partial L}{\partial \mathbf{w}} = 0 \rightarrow \mathbf{S}\mathbf{w} - \lambda \mathbf{w} = 0 \\ \therefore (\mathbf{S} - \lambda \mathbf{I})\mathbf{w} = 0 $$

PCA의 해에서 $\mathbf{w}$는 $\mathbf{S}$의 고유 벡터가 되고, $\lambda$는 $S$의 고유 값이 된다.

 

Step 4. Find the base set of bases

우리는 $\mathbf{w}$에 원래 벡터를 projection 후 분산의 변화량을 계산할 수 있다.

$$ \mathbf{S}\mathbf{w}{1} = \lambda{1}\mathbf{w}{1} \\ \mathbf{w}{1}^{T}\mathbf{S}\mathbf{w}{1} = \mathbf{w}{1}^{T}\lambda\mathbf{w}{1} = \lambda{1}\mathbf{w}{1}^{T}\mathbf{w}{1} = \lambda_{1} $$

$\mathbf{S}$ 대신 고유 벡터인 $\lambda$를 쓸 수 있고, 이는 스칼라이기 때문에 왼쪽으로 빼줘서 결국 $\lambda$만 남게 된다.

이를 통해 알 수 있는 사실은 결국 분산의 변화량은 $\lambda$가 되는 것이다.

따라서 $\frac{\lambda_{1}}{\lambda_{1}+\lambda_{2}}$를 통해 분산의 보존량을 구할 수 있다.

Step 5. Extract new features

우리는 step 4에서 bases를 뽑았으니 이를 통해 새로운 feature를 추출해야 한다.

위에서 구한 $\mathbf{w}$를 $\mathbf{x}$ 에 곱해 $\mathbf{z}$를 구한다.

위 결과에서 $\mathbf{z}{1}$은 $\mathbf{w}{1}^{T}\mathbf{X }$이다. 위 연산을 통해 PC를 구한다.

Step 6. Reconstruct the original data

$\mathbf{w}^{T}\mathbf{X}$에 $\mathbf{w}$를 다시 곱함으로써 다시 원본 데이터로 reconstruction 할 수 있다.

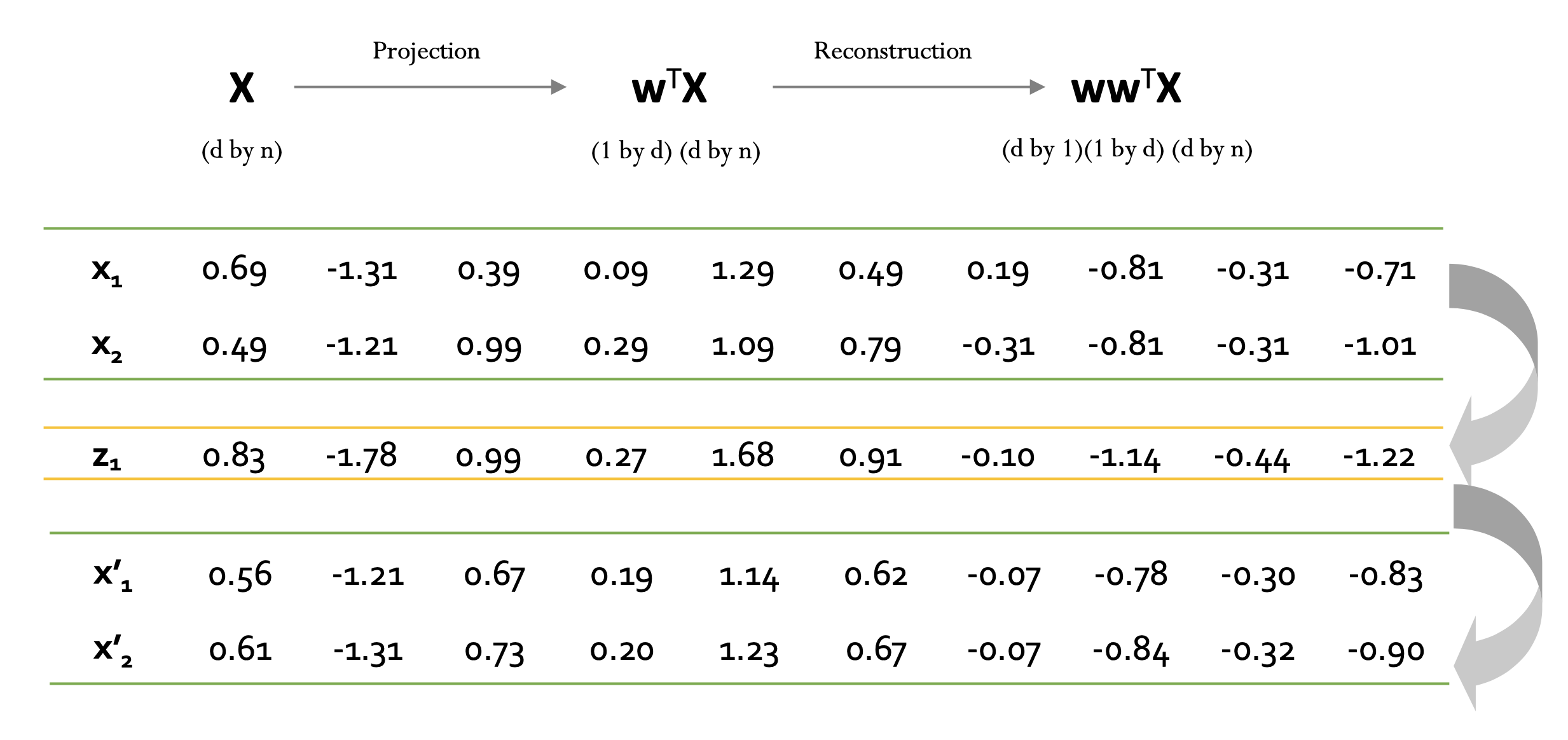
위 결과와 마찬가지로 $\mathbf{x}$와 $\mathbf{x}'$ 사이 약간의 오차가 발생하게 되는데, 해당 오차를 가지고 anomaly detection 분야에서 활용할 수 있다.

이 과정을 통해 PCA의 모든 절차를 알아보았다.

PCA에 대한 몇 개의 이슈가 남아 있는데, 가장 중요한 것은 PCA는 구체적인 몇 개의 component를 가지고 최적화해야 하는지에 대한 정해진 답은 없다. 보통 분산에 대한 보존량 비율 또는 전문가의 의견을 통해 판단한다.

PCA에 대한 한계점은 통계적 모델이라 데이터의 분포가 가우시안이라는 것을 가져해야 한다. 데이터가 가우시안 분포를 따를 때는 정상적으로 작동하지만, multimodal과 같은 분포를 따른다면 작동이 안 될 수 있다. 또한 PCA는 분류에 대한 목적으로 사용하지 않는다.