| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- SVM 이란
- fast r-cnn
- CNN
- pytorch
- Faster R-CNN
- CS231n
- SVM hard margin
- yolov3
- EfficientNet
- pytorch c++
- computervision
- pytorch project
- 데이터 전처리
- 논문분석
- self-supervision
- yolo
- TCP
- cs231n lecture5
- svdd
- support vector machine 리뷰
- libtorch
- RCNN
- SVM margin
- Object Detection
- DeepLearning
- 서포트벡터머신이란
- darknet
- Deep Learning
- cnn 역사
- Computer Vision
- Today
- Total
아롱이 탐험대
NMF의 기본 이론과 이해 본문
NMF (Non-netgative Matrix Factorization)
: 음수를 포함하지 않는 행렬 $X$를 음수를 포함하지 않는 행렬 $W$와 $H$의 곱으로 분해하는 알고리즘이다.
$$ X = WH$$
$$X\in \mathbb{R}^{m \times n} \\
where \ m: Num \ of \ data samples, \ n: Dimension \ of \ data \ samples$$
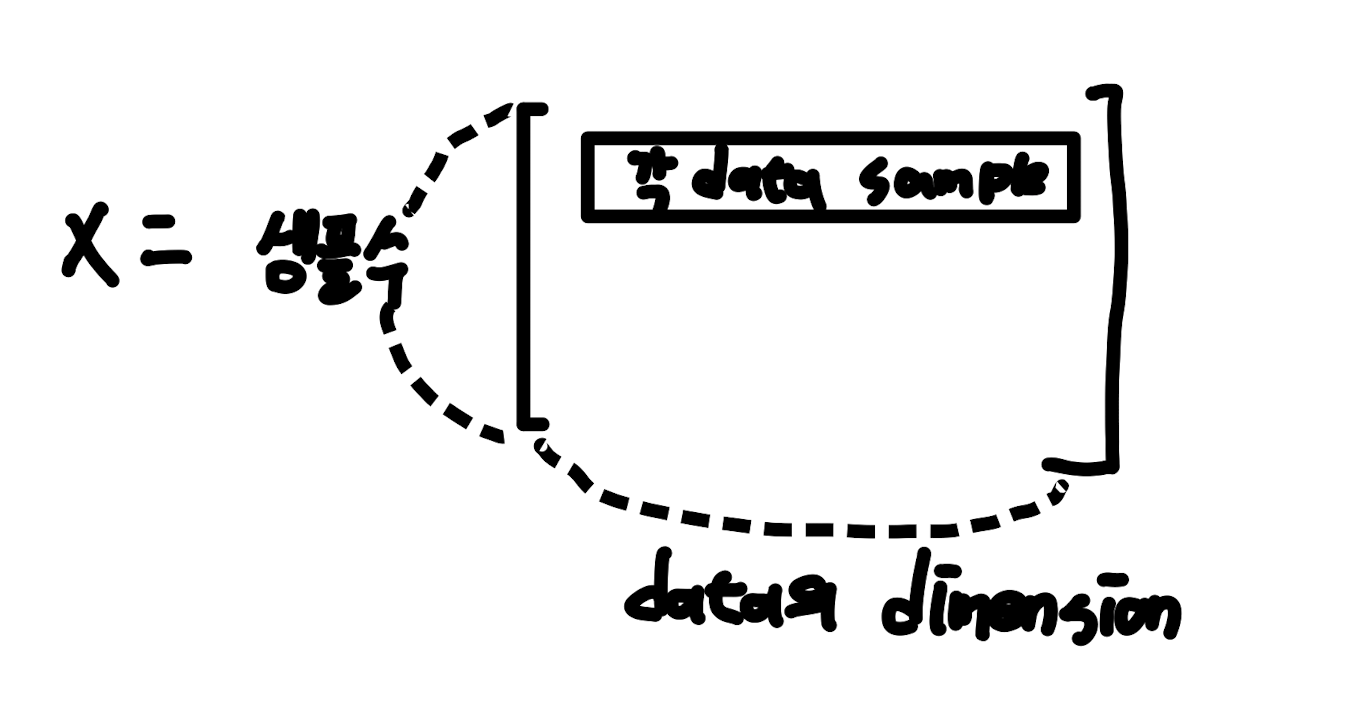
만약 $p$개의 feature를 가지고 원래의 $data \ set \ X$를 분해한다면
$$W\in \mathbb{R}^{m \times p}, \ H \in \mathbb{R}^{p \times n} $$

NMF는 다른 분해법과는 달리 분해 후 non-netgativity 특성을 보존할 수 있고, PCA 및 SVD에 비해 각 feature들의 독립성을 잘 습득 할 수 있다. (PCA, SVD는 직교성이 보장되는 대신 feature vector들이 서로 직교하게 된다면 dataset의 실제 구조를 잘 반영하기 힘들다.)
사전 지식
(1) trace (대각합 연산)
$$A =
\begin{pmatrix}
a_{11} \ a_{12} \ a_{13}\\
a_{21} \ a_{22} \ a_{23}\\
a_{31} \ a_{32} \ a_{33}
\end{pmatrix} \Rightarrow tr(A) = a_{11}+a_{22}+a_{33}$$
$$tr(A+B) = tr(A) + tr(B) \\ tr(ABC) = tr(CAB) = tr(BCA) = \cdots = tr(CBA)$$
$$\triangledown x\ tr(AX) = A^T \\
\triangledown x\ tr(X^{T}A) = A \\
\triangledown x\ tr(X^{T}AX) = (A+A^{T})X \\
\triangledown x\ tr(XAX^{T})= X(A^{T}+A)$$
(2) Frobenius norm
$$A = \begin{pmatrix}
a \ b \\
c \ d
\end{pmatrix}
\rightarrow \| A\|_{F}= \sqrt{a^2 + b^2+c^2+d^2}$$
$$A^TA =\begin{pmatrix}
a \ c \\
b \ d
\end{pmatrix} \begin{pmatrix}
a \ b \\
c \ d
\end{pmatrix}
= \begin{pmatrix}
a^2+c^2 \ ab+cd \\
ab+cd \ b^2+d^2
\end{pmatrix} $$
$$\rightarrow \|A\|_{F} = \sqrt{tr(A^TA)}$$
$$\therefore \|A\|_{F} = \sqrt{\sum^m_{i=1} \sum^n_{j=1}\|a_{ij}\|^2} = \sqrt{tr(A^TA)}$$
(3) Element-wise product
$$A = \begin{pmatrix}
1 \ 2 \\
3 \ 4 \\
\end{pmatrix}, B = \begin{pmatrix}
a \ b \\
c \ d \\
\end{pmatrix} \\ \\
A \circ B = \begin{pmatrix}
1a \ 2b \\
3c \ 4d \\
\end{pmatrix}$$
NMF의 update 규칙
$$H:= H\circ \frac{W^TX}{W^TWH} \\
W:= W\circ \frac{XH^T}{WHH^T}$$
유도과정
: X를 분해해서 얻은 W, H는 최대한 X에 가까워야 한다.
$\|X-WH\|^2_{F} = tr((X-WH)^T(X-WH)) \cdots Frobenius \ norm$
$\rightarrow H := H - \eta H\circ \triangledown_{H}\|X-WH\|^2_{F} \\
\ \ \ \ \ W := W - \eta W\circ \triangledown_{W}\|X-WH\|^2_{F} \ \cdots gradient \ descent \ \ \ (a)$
interative한 방식으로 분해를 진행한다.
Frobenius norm으로 표현한 수식을 아래와 같이 전개한다.
$\|X-WH\|^2_{F} = tr((X-WH)^T(X-WH)) \\
= tr((X^T - H^TW^T)(X - WH)) \\
= tr(X^TX - X^TWH-H^TW^TX+H^TW^TWH)$
이를 통해 $\triangledown_{H}\|X-WH\|^2_{F}, \ \triangledown_{W}\|X-WH\|^2_{F}$ 를 아래와 같이 전개한다.
$\triangledown_{H}\|X-WH\|^2_{F} = \triangledown H\{ tr(X^TX) \ -tr(X^TWH) \ -tr(H^TW^TX) + tr(H^TW^TWH) \} \\
= 0 \ -(X^TW)^T -W^TX + (W^TW+(W^TW)^T)H \\
= -2W^TX+2W^TWH \cdots (b)$
$\triangledown_{W}\|X-WH\|^2_{F} = \cdots \\
= -2XH^T +2WHH^T \cdots (c)$
$(a)$에 $(b), \ (c)$를 대입한다. (상수곱은 무시)
$H := H + \eta H\circ (W^TX - W^TWH) \\
W := W + \eta W\circ (XH^T - WHH^T)$
이 과정에서 뒤 term에 음수가 포함되므로 특별한 방식의 gradient descent를 수행한다.
$\rightarrow$ learning rate인 $\eta$를 data-driven하게 정의한다.
$$\eta_{H} =\frac{H}{W^TWH}, \ \eta_{W} = \frac{W}{WHH^T} \\
\rightarrow H := H + \frac{H}{W^TWH} \circ (W^TX - W^TWH) \\
= H + H \circ \frac{W^TX}{W^TWH} - H \circ \frac{W^TWH}{W^TWH}$$
$\frac{W^TWH}{W^TWH} = I , \ H \circ \frac{W^TWH}{W^TWH}=H$이므로
$$\rightarrow H+ H \circ\frac{W^TX}{W^TWH}- H = H \circ \frac{W^TX}{W^TWH} \\
\therefore H := H \circ \frac{W^TH}{W^TWH} \\
\therefore W := W \circ \frac{XH^T}{WHH^T}$$
Reference
'study > linear algebra' 카테고리의 다른 글
| Broadcasting, Sparse matrix의 기본 이론과 이해 및 활용 (0) | 2022.02.22 |
|---|---|
| SVD의 기본 이론과 이해 및 활용 (1) | 2022.01.21 |


