| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Object Detection
- 서포트벡터머신이란
- pytorch
- yolo
- SVM hard margin
- support vector machine 리뷰
- CNN
- Computer Vision
- Deep Learning
- svdd
- fast r-cnn
- CS231n
- libtorch
- 데이터 전처리
- computervision
- cs231n lecture5
- self-supervision
- RCNN
- Faster R-CNN
- pytorch c++
- 논문분석
- TCP
- SVM margin
- SVM 이란
- pytorch project
- EfficientNet
- yolov3
- cnn 역사
- darknet
- DeepLearning
- Today
- Total
아롱이 탐험대
[Anomaly Detection] Local Outlier Factor (LOF) 본문
본 포스트는 고려대학교 산업경영공학부 강필성 교수님의 Business Analytics 강의를 정리한 내용입니다.
LOF (Local Outlier Factor)는 밀도 기반 이상치 탐지의 방법론 중 하나이다.
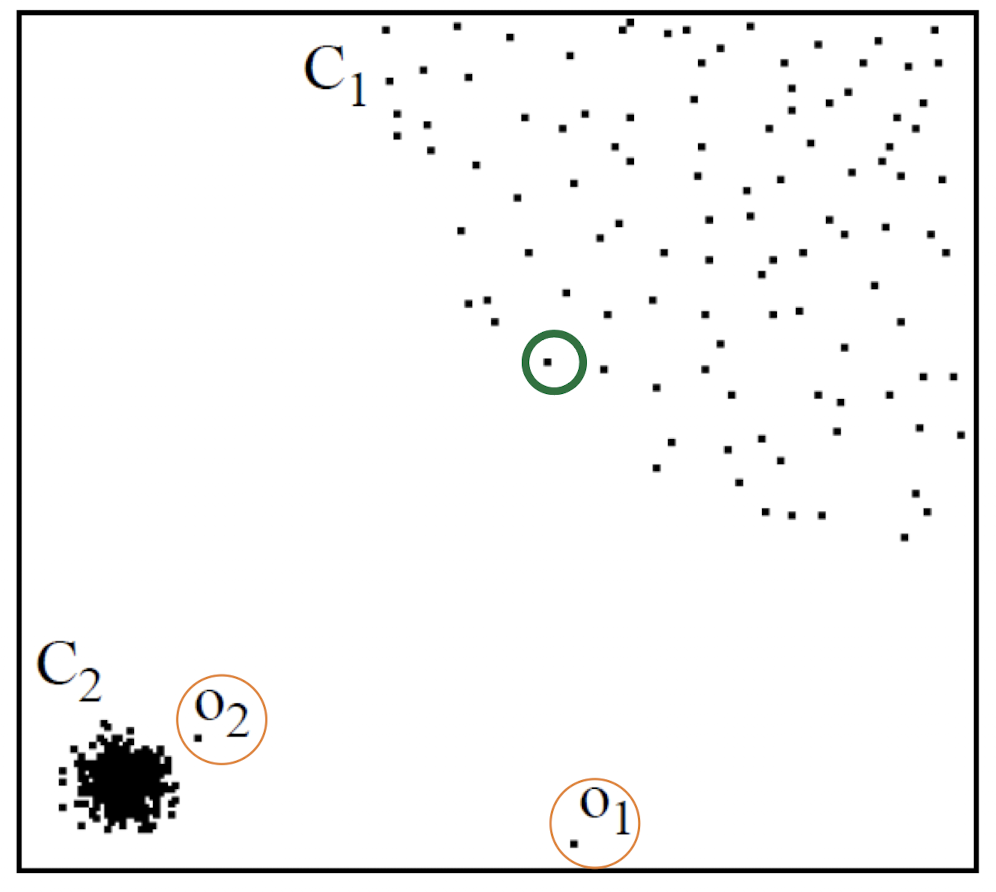
위 plot을 보면 $C_{1}$ 부근 영역은 상대적으로 밀도가 낮은 영역이고, $C_{2}$ 부근 영역은 상대적으로 높은 밀도를 가지고 있다.
여기서 $o_{1}$의 경우는 누가 봐도 이상치에 해당하는 값이다. 하지만 $o_{2}$의 경우에는 neighborhood와의 거리가 짧은 곳에 위치해 있다. 초록색 원이 $o_{3}$라고 할 때 $o_{2}$의 neighborhood 간 거리가 $o_{3}$의 neighborhood 거리보다 더 클 것이다. 따라서 이 2개만 비교하면 $o_{2}$는 abnormal, $o_{3}$는 상대적으로 normal으로 분류가 될 것이다.
우리의 목표는 위와 같이 $o_{2}$의 abnormal score가 $o_{3}$의 abnormal score보다 더 크게 측정하는 것이다.
LOF는 5가지의 definition에 대해 순차적으로 계산이 된다.
Definition 1) k-distance of an object $p$
Object $p$의 $p$는 point를 의미하고, $k\text{-distance}$ $k$는 자연수이다.
$d(p,q)$는 관측치 $p$와 $q$의 거리를 의미한다.
$k\text{-distance}(A)$는 $A$로부터 $K$번째 근접 이웃까지의 거리를 의미한다.
관측치 $p$의 $k\text{-distance}$는 $d(p,o)$의 distance로 정의된다. 여기서 2가지의 조건이 있는데 다음과 같다.
- 최소한 $k$개의 object $o'$에 대해서는 $p$와 $o'$의 거리는 $p$와 $o$까지의 거리보다 작거나 같아야 한다.
$$ d(p, o') \leq d(p,o) $$
- 최대로 $k-1$개에 object $o'$에 대해서는 아래의 수식을 만족해야 한다.
$$ d(p,o') < d(p,o) $$
동률을 고려해서 정렬을 했을 때 $k$에 해당하는 거리이다.

위 그림을 예시로 $p$에 대한 3-distance를 계산해보자.
가장 가까운 이웃 간 거리는 순차적으로 0.5, 1.0, 1.5, 1.5, 1.5이다.
3-distance는 최소한 3개 이상의 객체에 대해서는 $p$에 해당하는 객체 거리보다는 작거나 같아야 하고, 최대 $k-1$개까지의 거리는 3 distance보다 작아야 한다.
3-distance를 만족하는 객체는 0.5, 1.0, 1.5이다. k-distance는 1.5가 된다.
자신 $p$를 제외하고 3-distance인 1.5보다 작거나 같은 $o'$는 5개이고, 여기서 5개는 $k(3)$보다 작거나 같고, 2개는 $k(3)$보다 작다.
이 경우에는 3-distance가 1.5가 되고, 이에 따라 동률을 고려할 때 $k$번째의 거리가 3-distance가 된다.

위 그림과 같은 경우에는 3-distance는 1.0이 된다.

3-distance는 1.0이 된다.
Definition 2) k-distance neighborhood of an object p
$$ N_{k}(p) = \{ q\in D(p) \mid d(p,q) \leq k\text{-distance}(p) \} $$
두 번째 정의는 object $p$의 k-distance neighborhood이다. 이는 위 수식으로 정의된다.
$p$라는 객체의 k-distance가 주어졌을 때 $p$의 k-distance neighborhood인 $q$의 distance는 k-distance($p$) 보다 같거나 작다라는 의미이다.

위 그림을 보면 3-distance($p)$는 1.5인 것을 알 수 있고, 수식에 따라 $N_{3}(p)$는 총 5개인 것을 확인할 수 있다.
Definition 3) Reachability distance
세 번째 정의는 reachability distance, 즉 도달 가능 거리이다.
Reachability distance를 구하는 수식은 다음과 같다.
$$ \text{reachability-distance}_{k}(p,o) = \max{\{k\text{-distance}(o), d(p,o)\}} $$
수식을 해석하면 $o$의 k-distance와 $p$와 $o$의 distance 중 최대 값이 도달 거리라는 의미이다.

object $A$를 기준으로 neighborhood가 위 그림처럼 주어져있다고 하자.
$A$와 $C$를 기준으로 하였을 때 reachability distance는 $C$에서부터 $A$까지의 distance는 k-distance$(A)$보다 작기 때문에 reachability distance를 k-distance$(A)$로 설정한다.
$A$와 $B$는 서로 같기 때문에 둘 중 아무것이나 선택한다.
$A$와 $D$의 경우 $d(A,D)$가 더 크기 때문에 reachability distance는 위 그림과 같아진다.
Definition 4) Local reachability density of an object p
$$ lrd_{k} = \frac{\mid N_{k}(p)\mid}{\sum_{o \in N_{k}(p) }reachability-distance_{k}(p,o)} $$
4번째 정의는 LRD (Local Reachability Density)이다. 수식은 위와 같이 정의된다.
$p$를 기준으로 이웃으로 속하는 $o$에 대한 도달 가능 거리 분의 $N_{k}(p)$로 정의된다.
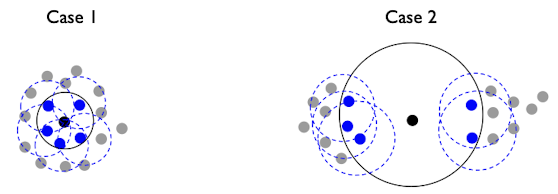
이를 위 그림을 보며 이해해보자.
case 1에서 검은색 점 $p$에 대한 reachability distance는 검정색 반경이고, $p$의 이웃인 파란색 점들에 대한 reachability distance는 파란 점선 반경이다.
case 2에서는 case 1에 비해 이웃 점들이 멀리 떨어져 있다. 이런 경우에는 case 1에 비해 $lrd_{k}$의 값이 작아지게 된다.
Definition 5) Local outlier factor of an object p
LOF (Local Outlier Factor)는 실질적으로 계산을 해야 하는 식이고, 수식은 다음과 같이 정의된다.
$$ LOF_{k}(p) = \frac{\sum_{o \in N_{k}(p)} \frac{lrd_{k}(o)}{lrd_{k}(p)}}{\mid N_{k}(p)\mid} = \frac{\frac{1}{lrd_{k}(p)}\sum_{o \in N_{k}(p)}lrd_{k}(o)}{\mid N_{k}(p)\mid} $$
$LOF$는 아래 그림과 같이 $lrd_{k}(p)$와 $lrd_{k}(o)$에 크기의 따라 커지거나 작아진다.

point들의 density의 따라 값이 변화하는 모습을 볼 수 있다.
case 3을 보면 상대적 밀도는 크다. 하지만 $lrd_{k}$를 계산하게 되면 밀도가 낮은 영역이기 때문에 $p, o$에 대한 $lrd_{k}$가 작아지게 된다.
case 2는 $p$의 관점에서 밀도가 낮기 때문에 작지만 $o$를 기준으로 하면 상대적으로 밀도가 크다. 따라서 $lrd_{k}$가 크게 나온다.
이를 통해 밀도가 낮은 영역의 abnormal score를 높게 만들고, 밀도가 충분히 높은 영역의 score를 작게 만들 수 있다.

따라서 위 plot의 LOF를 적용하여 abnormal score를 적용하면 다음과 같이 된다.
밀도가 낮은 영역의 score는 크고, 밀도가 큰 영역의 score는 작은 모습을 볼 수 있다.
하지만 무조건 밀도가 낮다고 해서 score가 큰 것은 아니다. 이웃 간 거리도 반영하여 score를 결정하기 때문이다.
이를 통해 LOF를 이용하여 밀도 기반 abnormal score를 계산해보았다.
LOF는 상당히 오래된 논문이다. 계산 복잡도가 좋지 않다는 단점을 가지고 있고, 이보다 더 큰 단점은 score가 normalization 되어 있지 않다.
이는 데이터 셋마다 분포가 달라, 각 셋 마다 지표의 정도가 달라질 수 있다.
→ 명확한 기준이 없다는 의미이다.
'study > IME654' 카테고리의 다른 글
| [Anomaly Detection] Distance, Clustering, PCA-based Methods (0) | 2022.07.11 |
|---|---|
| [Anomaly Detection] Parzen Window Density Estimation (0) | 2022.07.10 |
| [Anomaly Detection] Gaussian Density Estimation & Mixture of Gaussian Density Estimation (0) | 2022.07.08 |
| [Anomaly detection] Overview (0) | 2022.04.29 |
| [Dimensionality Reduction] Overview (0) | 2022.03.15 |




