| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- EfficientNet
- cs231n lecture5
- fast r-cnn
- computervision
- RCNN
- Faster R-CNN
- Computer Vision
- DeepLearning
- Object Detection
- cnn 역사
- CS231n
- yolov3
- pytorch project
- Deep Learning
- self-supervision
- SVM hard margin
- yolo
- pytorch c++
- TCP
- 서포트벡터머신이란
- SVM 이란
- 논문분석
- darknet
- pytorch
- CNN
- svdd
- SVM margin
- libtorch
- 데이터 전처리
- support vector machine 리뷰
- Today
- Total
아롱이 탐험대
Machine learning: probability (Multivariate Gaissian ~ Transformation of Random Variables) 본문
Machine learning: probability (Multivariate Gaissian ~ Transformation of Random Variables)
ys_cs17 2022. 4. 10. 20:16Multivariate Gaussian
Multivariate이란 다차원이라는 말이다. R.V. $\text{x}$가 다차원일 때 Gaussian distribution은 아래 수식과 같이 구한다. 크게 틀은 달라지지 않는다.

$\mu = \mathit{\mathbb{E}}[\text{x}] \in \mathit{\mathbb{E}}^{D}$ is the mean vector. D차원의 $\text{x}$의 평균값
$\sum = \text{cov[\text{x}]}$는 $D \times D$ 크기의 covariance matrix이다.
parameter의 개수는 우리가 어떤 covariance matrix를 사용하냐에 따라 다르다.
(1) Full covariance: 행렬이 대칭적이기 때문에 $\frac{D(D+1)}{2}$개의 parameter가 필요하다.
(2) Diagonal covariance: 0인 부분을 제외한 diagonal covariance의 parameter의 개수는 $D$이다.
(3) Spherical covariance: Spherical covariance는 diagonal element의 값들이 시그마 제곱과 같다. 따라서 parameter의 개수는 다음과 같다. $\sum = \sigma^{2}I_{D}$

그림에서 (a)는 Full covariance인데 이를 시각화하면 타원형 등고선의 모습을 볼 수 있다. (b)는 Diagonal covariance인데 축으로 정렬된 타원과 같이 시각화되고, (c)인 spherical covariance matrix는 원형의 모습을 한 것을 볼 수 있다. (d)는 spherical Gaussian의 surface plot이다.
Dirichlet Distribution
Dirichlet distribution은 beta distribution의 multivariate 버전이라고 생각하면 된다.
Dirichlet에 들어가는 $K$차원의 continous R.V. $x$에 대한 set에 대한 정의는 다음과 같다.
$$S_{K} = \left\{x:0≤x_{k} ≤ 1, \sum^{K}{K}x{k} = 1 \right\}$$
모든 $x$의 값은 0과 1사이에 존재하는 실수이고, $x$들의 합은 1이다. 확률의 정의와 같다.
Dirichlet distribution의 식은 다음과 같다.
$$\text{Dir}(x \mid \alpha) = \frac{1}{\beta(\alpha)}\prod_{K =1}^{K}{x_{K}^{\alpha_{K}-1}}$$

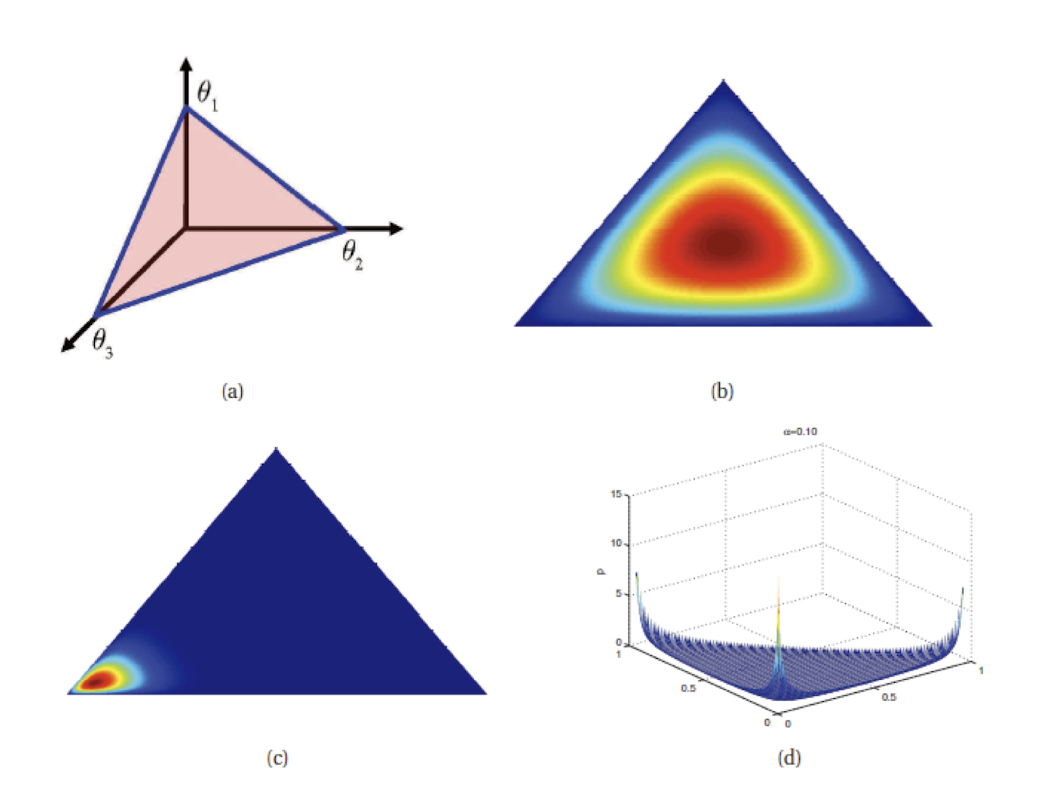
$K$=3 인 경우에 Dirichlet distribution을 도식화 한 그림이다. (a)를 보면 $K=3$이기 때문에 삼각형 모양으로 나타내진 모습을 볼 수 있고, 각 point인 $\theta$ 값은 0보다 크고 1보다 작은 값이다. 여기서 $\mathbf{\alpha}0=\sum{k=1}^K\mathbf{\alpha}k$은 peak가 얼마나 높은지를 제어하고, $\alpha{k}$는 peak의 위치를 제어한다. 예를 들어 $\text{Dir}(1,1,1)$은 uniform distribution이고, $\text{Dir}(2,2,2)$는 $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$을 중심으로 하는 좁은 distribution이다.
모든 $K$에 대해 $\alpha_{K} < 1$ 이면 simplex의 모서리에 spike가 나타난다. 정리하자면 \alpha_{K} 값이 증가하면 $\text{var}[x]$이 감소하는 것을 볼 수 있다.
Dirichlet distribution은 다음과 같은 특성을 같는다.
$$ \begin{align}\mathbb{E}[x_k]=\frac{\alpha_k}{\alpha_0},\quad\text{mode}[x_k]=\frac{\alpha_k-1}{\alpha_0-K},\quad\text{var}[x_k]=\frac{\alpha_k(\alpha_0-\alpha_k)}{\alpha_0^2(\alpha_0+1)}\end{align} $$
대부분 symmetric한 경우를 가정하고 확률을 구하는데, symmetric Dirichlet prior는 $\alpha_{K}= \frac{\alpha}{K}$ 형태를 갖는다. 이러한 경우 $\text{mean}=1/K,\ \text{var}[x_k]=\frac{K-1}{K^2(\alpha+1)}$가 되는데, $\alpha$ 값이 증가할 수록 distribution의 precision이 증가하고, narrow해지며, variance가 줄어들게 된다.
Transformation of Random Variables
$x\sim p()$를 따르는 random variable에 대해 $y = f(x)$일때 y의 distribution이 무엇인지를 구하는 게 transformation of random variables의 핵심이다.
Linear transformation
만약 $f$가 선형 함수이면 $y = f(x) = Ax + b$의 형태를 갖는다. $A, b$는 어떠한 matrix이다.
$f:x\in R^D\rightarrow y\in R^D$ 이를 general function이라고 한다.
$f$가 만약 linear function이면 아래의 속성을 갖게 된다.
$$ \begin{align}\mathbb{E}[\mathbf{y}]=\mathbb{E}[\mathbf{Ax+b}]=\mathbf{A{\mu}+b}\\ \text{cov}[\mathbf{y}]=\text{cov}[\mathbf{Ax+b}]=\mathbf{A\Sigma A}^T\end{align} $$
여기서 $\mu = \mathbb{E}[x]$는 linearity of expectation이라고 부르고, $\sum= cov[x]$이다.
만약 $f$ 가 scalar valued function이면 (1차원인 경우) $f(x) = a^{T}x + b$ 형태로 쓸 수 있는데, a와 b는 각 $(1 \times D), (D \times 1)$이고, 이 때의 mean과 variance는 다음과 같다.
$$f:x\in R^D\rightarrow y\in R^1$$
$$ \begin{align}\mathbb{E}[\mathbf{y}]=\mathbb{E}[\mathbf{a}^T\mathbf{x}+b]=\mathbf{a}^T{\mu}+b\\ \text{var}[y]=\text{var}[\mathbf{a}^T\mathbf{x}+b]=\mathbf{a}^T\mathbf{\Sigma a}\end{align} $$
하지만 mean과 covarance는 $x$가 Gaussian인 경우에만 $y$의 distribution을 완전하게 정의한다는 점에 유의해야한다. 일반적으로 $y$의 distribution을 도출하기 위해 general transformation을 이용해야 한다.
General Transformation (for Discrete R.V.)
만약 $x$가 discrete random variable일 때, $y$에 대한 pmf를 $f(x) = y$를 만족하는 모든 $x$에 대해 probability mass를 더하는 방식으로 도출해낼 수 있다.
수식은 아래와 같다.
$$p_{y}(y) = \sum_{x:f(x)=y}p_{x}(x)$$
$p_{x}(x)$가 $\text{set} = \left\{1,2, \cdots, 10\right\}$에서 uniform이므로, $p_{x}(x) = 0.1$이고, 위 식에 적용하여 $p_{y}(1), p_{y}(0)$을 구할 수 있다.
$$ \quad p_y(1)=\sum_{x\in\{2,4,6,8,10\}}p_x(x)=0.5\\ p_y(0)=0.5 $$
이 예시에서 f는 many to one function이다.
General Transformation (for Continous R.V.)
만약 $x$가 continuous R.V.라면 $p_{x}(x)$가 pmf가 아니라 density이기 때문에 위에서 정의한 수식을 사용할 수 없다. 그리고 density는 더할 수 없음으로 cdf를 이용해 $p_{y}(y)$를 다음과 같이 정의한다.
$$ \begin{align} P_y(y)\triangleq P(Y\le y)=P(f(X)\le y)=p(X\in\{x|f(x)\le y\}) \end{align} $$
이렇게 구한 cdf를 미분하게 되면 y에 대한 pdf를 구할 수 있다. 이때 f가 monontonic이고, 역함수가 존재한다면 p_{y}(y)를 다음과 같이 쓸 수 있다.
$$ \begin{align} P_y(y)=P(f(X)\le{y})=P(X\le{f^{-1}}(y))=P_x(f^{-1}(y))\quad\text{by def. of cdf}\ \end{align} $$
위 식을 미분하게 되면 다음의 식을 얻을 수 있다. 여기서 $x = f^{-1}(y)$이다.
$$ \begin{align} p_y(y)\triangleq\frac{d}{dy}P_y(y)=\frac{d}{dy}P_x(f^{-1}(y))=\frac{dx}{dy}\frac{d}{dx}P_x(x)=\frac{dx}{dy}p_x(x) \end{align} $$
여기서 dx를 x-space의 volume measure로 생각할 수 있다. 마찬가지로, dy는 y-space의 volume measure이다. 따라서 \frac{dx}{dy}는 volume의 변화를 측정한다. 이때 부호가 바뀌는 것은 중요하지 않으므로 절대값을 취하여 다음의 general expression을 얻게 된다.
$$ \begin{align} p_y(y)=p_x(x)\left|\frac{dx}{dy}\right| \end{align} $$
이 식을 change of variable 공식이라고 한다. 이 결과를 다음과 같이 보다 직관적으로 이해할 수 있다.
$p_x(x)\delta{x}\approx{p_y(y)\delta{y}}$에 의해 범위 $(x, x+\delta{x})$에 속하는 관측값은 $(y, y+\delta{y})$로 transform 된다. 따라서 $p_y(y)\approx{p_x(x)\left|\frac{\delta{x}}{\delta{y}}\right|}$가 된다.
예를 들어, $X\sim{U(-1,1)}$ 이고 $Y=X^2$ 이라고 할 때, $p_y(y)=\frac{1}{2}y^{-\frac{1}{2}}$를 얻을 수 있다.
Multivarate change of variables
general transformation의 결과를 multivariate distribution으로 확장해보자.
$f: R^n\rightarrow R^n$이고, $y = f(X)$라고 할 때, 이에 대한 Jacobian matrix $J$는 아래와 같은 식으로 주어진다.
$|det \ J|$는 $f$를 적용했을 때, unit cube의 부피 변화량을 측정한다. 만약 mapping $f$가 invertible mapping이라면 nverse mapping $y → x$의 Jacobian을 이용해 transformed variables의 pdf를 정의할 수 있다.
$$ \begin{align} p_y({y})=p_x({x})\left|\text{det}\left(\frac{\partial{x}}{\partial{y}}\right)\right|=p_x({x})|\text{det}\ {J_{y\rightarrow{x}}}| \end{align} $$
간단한 예시로 Cartesian coordinates $x = (x_{1}, x_{2})$에서 polar coordinates $y = (r, \theta)$로의 density transforming을 살펴보자. 여기서 $x_{1} = r\cos{\theta}$이고 $x_{2} = r\sin{\theta}$이다.
그러면 Jacobian matrix는 다음과 같이 쓸 수 있다.
$$ {J_{y\rightarrow{x}}}= \begin{pmatrix} \frac{\partial{x_1}}{\partial{r}}& \frac{\partial{x_1}}{\partial{\theta}}\\ \frac{\partial{x_2}}{\partial{r}}& \frac{\partial{x_2}}{\partial{\theta}} \end{pmatrix}= \begin{pmatrix} \text{cos}\theta&-r\text{sin}\theta\\ \text{sin}\theta&r\text{cos}\theta \end{pmatrix}\\{}\\ |\text{det }{J}|=|r\text{cos}^2\theta+r\text{sin}^2\theta|=|r| $$
따라서 $p_{y}(y)$를 구하게 되면 다음과 같이 나타낼 수 있다.
$$ p_{{y}}({y})=p_{{x}}({x})|\text{det }{J}|=p_{{x}}({x})|r|\\ p_{r,\theta}(r,\theta)= p_{x_1,x_2}(x_1,x_2)r=p_{x_1,x_2}(r\text{cos}\theta,r\text{sin}\theta)r $$
이것을 기하학적으로 보게 되면 아래의 그림처럼 나타낼 수 있다.

그림에서 검정색 부분의 면적은 다음과 같이 주어진다.
$$ \begin{align} P(r\le{R}\le{r+dr},\theta\le{\Theta}\le\theta+d\theta)=p_{r,\theta}(r,\theta)drd\theta \end{align} $$
극한에서, 이것은 patch의 중심에서의 density인 $p_{r, \theta}(r, \theta)$와 patch의 크기 $r, dr, d\theta$를 곱한 것과 같다.
따라서 다음 식을 얻을 수 있다.
$$ \begin{align} p_{r,\theta}(r,\theta)drd\theta=p_{x_1,x_2}(r\text{cos}\theta,r\text{sin}\theta)r\ dr\ d\theta \end{align} $$
'study > Machine Learning' 카테고리의 다른 글
| Machine learning: Logistic Regression (MLE ~ Multi-class Logistic Regression) (0) | 2022.05.09 |
|---|---|
| Machine learning: Linear Regression (MLE) (0) | 2022.04.28 |
| Machine learning: probability (Central limit theorem ~ MIC) (0) | 2022.04.12 |
| Machine learning: probability (Discrete Random Variables~Covariance and Correlation) (0) | 2022.04.06 |
| Machine learning overview (0) | 2022.04.02 |




