| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 데이터 전처리
- self-supervision
- CNN
- pytorch project
- Deep Learning
- support vector machine 리뷰
- SVM hard margin
- RCNN
- pytorch
- cnn 역사
- pytorch c++
- CS231n
- SVM margin
- 서포트벡터머신이란
- 논문분석
- yolo
- Faster R-CNN
- computervision
- fast r-cnn
- libtorch
- TCP
- SVM 이란
- Object Detection
- EfficientNet
- yolov3
- cs231n lecture5
- darknet
- DeepLearning
- Computer Vision
- svdd
- Today
- Total
아롱이 탐험대
Machine learning: probability (Central limit theorem ~ MIC) 본문
Machine learning: probability (Central limit theorem ~ MIC)
ys_cs17 2022. 4. 12. 22:20Central limit theorem
각각 평균 $\mu$와 분산 $\sigma^{2}$ 에 대한 probability density function인 $p(x_{i})$를 갖는 $\text{R.V.}$에 대해 생각해보자.
각 variable이 independent이고, i.i.d. (identically distributed)라고 가정하자.
$S_{N} = \sum_{i = 1}^{N}X_{i}$은 random variable의 합이고, 이는 간단하지만 널리 사용되는 random variable의 transformation이다. N이 증가할수록, S_{N}의 distribution은 아래 식과 가까워진다는 것을 알 수 있다. 다시 말해, 주어진 조건에서 N이 증가할수록 Gaussiam distribution의 형태를 띠게 된다.
$$ p(S_N=s)=\frac{1}{\sqrt{2\pi{N}\sigma^2}}\text{exp}\left(-\frac{(s-N\mu)^2}{2N\sigma^2}\right) $$
따라서 distribution of the quantity는 다음과 같다.
$$ Z_N\triangleq\frac{S_N-N\mu}{\sigma\sqrt{N}}=\frac{\overline{X}-\mu}{\sigma/\sqrt{N}} $$
여기서 $\overline{X}=\frac{1}{N}\sum_{i=1}^Nx_i$ 는 sample mean으로 standard normal로 수렴한다. 이것을 central limit theorem이라고 부른다.
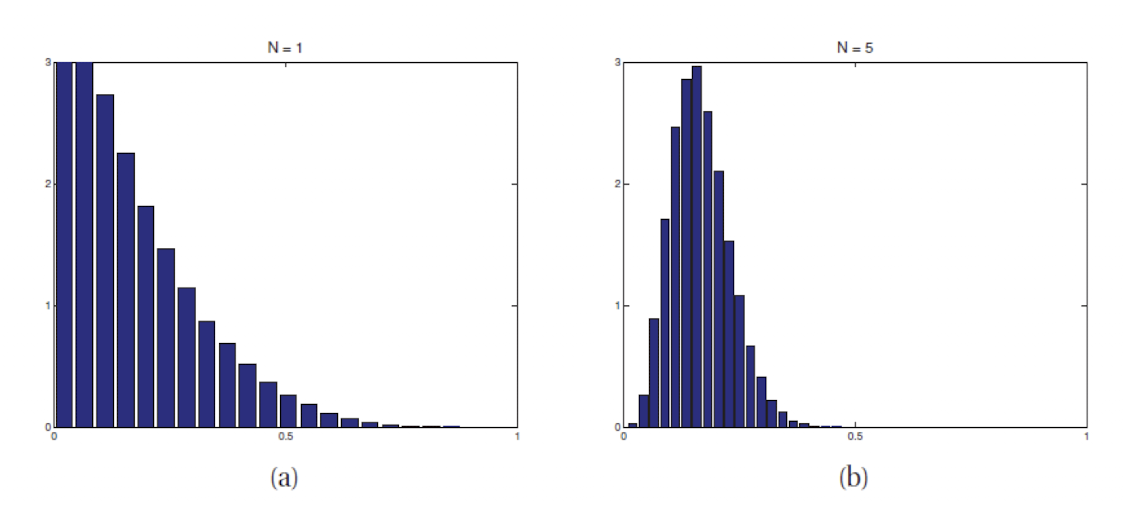
그림은 Beta 함수에 대해 central limit theorem을 적용했을 경우이다. (a)는 $N = 1,$ (B)는 $N = 5$이다.
$N$ 값이 점점 증가할 수록 Gaussian distribution의 형태를 띠게 되는 것을 볼 수 있다.
이러한 central limit theorem는 machine learning에서 굉장히 많이 사용된다. 어떤 영상을 분석할 때, 영상에 노이즈가 계속 추가된다면 결과적으로 노이즈는 Gaussian distribution 형태를 띨 것이라고 많이 가정한다.
실제로 통계적 모델링을 할 때, Gaussian assumption을 많이 하는 이유는 random variable의 합이 Gaussian distribution의 형태로 나타날 확률이 높기 때문이다. Machine learning에서도 i.i.d. assumption은 데이터들이 같은 generative process에 의해 sampling 되고, 데이터의 생성이 이전 데이터에 대해 독립적인 것이 일반적이기에 타당한 assumtion으로 취급하여 central limit theorem를 많이 사용한다.
Monte Calro Approximation
일반적으로, variable formula에 변화를 주어 R.V.의 function의 distribution을 계산하는 것은 간단하지 않을 수 있다. 이에 대한 간단하지만 강력한 대안은 다음과 같다.
먼저 distribution으로부터 $S$라는 sample를 생성하고 $S = \left\{x_{1}, \cdots, x_{S}\right\}$ 라고 한다. Sample이 주어졌을 때 $\left\{f(x_s)\right\}_{s=1}^S$의 empirical distribution을 사용하여 $f(X)$의 distribution을 근사할 수 있다. 이를 Monte calro approximation이라고 한다.
Monte calro approximation를 사용해서 R.V.의 어떤 함수의 기댓 값을 근사할 수 있다. 단순히 sample을 뽑은 다음 sample에 적용된 함수의 arithmetic mean을 계산하면 다음과 같이 쓸 수 있다.
$$ \mathbb{E}[f(X)]=\int{f(x)}p(x)dx\approx\frac{1}{S}\sum_{s=1}^S{f(x_s)} \text{, where }x_s\sim{p(X)} $$
식을 살펴보면 Monte calro approximation을 이용해서 어떤 함수의 value를 계산할 수 있다. 3 term의 수식과 마찬가지로 sample의 size로 나누어 approximation한다. $x_{x}$는 $p(X)$의 density를 따라야 한다.
$f$ 함수를 변환시켜 다음과 같은 여러 특성도 얻을 수 있다.
$$ \mathbb{E}[X] = \frac{1}{S}\sum_{S = 1}^{S}X_{S} $$
$$ \text{var}[X] = \frac{1}{S} \sum_{S=1}^{S}(x_{S} - \overline{x}), \ \ \overline{x} = \mathbb{E}[X] $$
$$ P(X ≤ C) = \frac{1}{S} \mid x_{S} ≤ C \mid $$
$$ \text{Median}(X) = \text{median}\left\{x_{1}, \cdots, x_{S}\right\} $$
Monte Calro Approximation Example

x에 대한 pdf는 맨 왼쪽 그래프와 같이 uniform이라고 가정하자. x_{s} \sim p(x)를 y=x^{2} 를 통해 Monte calro를 적용시키면 맨 오른쪽 그래프처럼 나온다. 실제 y=x^{2} 에 해당하는 그래프는 중간 그림인데, 이와 Monte calro 결과 히스토그램을 비교해보면 굉장히 유사하게 나온다.
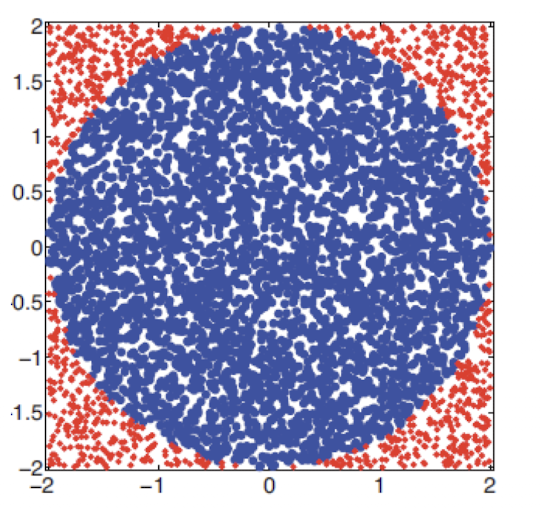
두 번째 예시이다. 원의 면적을 구해보자. 원의 면적을 $I$라고 하면 Indicator function을 사용하면 다음과 같다.
$$ \pi r^{2} = I = \int_{-r}^{r} \int_{-r}^{r} \mathbb{I}(x^{2}+y^{2} \leq r^{2})dxdy $$
Indicator function을 $f(x,y)$라고 하고, 원 밖에 점이 찍히면 0, 안에 찍히면 1의 값을 갖는 함수라고 하자. $p(x), p(y)$는 $[-r,r]$ 구간 내에 존재하는 균일 분포 함수이다. 따라서 $p(x) = p(y) = \frac{1}{2r}$이다.
$$ I = (2r)(2r)\int \int f(x,y)p(x)p(y)dxdy $$
$$ \approx 4r^{2} \frac{1}{S}\sum^{S}{i=1}f(x{i},y_{i}) $$
기본적으로 몬테카를로 근사법은 표본의 크기가 클수록 정확도가 높아진다. 실제 평균을 $\mu = E[f(X)]$라고 하자. 몬테카를로 근사법에 의한 근사 평균을 $\hat{\mu}$라고 하자. 독립된 표본이라는 가정 하에 아래와 같이 쓸 수 있다.
$$ (\mu - \hat{\mu}) → \mathcal{N}(0, \frac{\sigma^{2}}{S}) $$
$$ \sigma^{2} = \text{var}[f(X)] = E[f(X)^{2}] - E[f(X)]^{2} $$
위는 중심극한정리에 의한 결과이다. 물론 $\sigma^{2}$ 는 미지의 값이다. 그러나 이 또한 몬테카를로 적분에 의해 근사될 수 있다.
$$ \hat{\sigma^{2}} = \frac{1}{S}\sum^{S}{i = 1}(f(x{i}) - \hat{\mu})^{2} $$
$$ P(\mu - 1.96 \frac{\hat{\sigma}}{\sqrt{S}} ≤ \hat{\mu} ≤ \mu + 1.96\frac{\hat{\sigma}}{\ \sqrt{S}}) \approx 0.95 $$
이때 $\frac{\hat{\sigma}}{\ \sqrt{S}}$ 는 Numberical standart error라고 불리며, 이는 $\mu$ 의 추정량에 대한 불확실성에 대한 추정치이다. 만약 우리가 95%의 확률로 $\pm \epsilon$ 내부에 위치할 만큼 정확한 결과를 원한다면 $1.96 \frac{\hat{\sigma}}{\ \sqrt{S}} ≤ \epsilon$ 를 만족시키는 S개의 sample이 필요하다.
Information Theory
정보 이론은 데이터를 압축할 때 주로 사용한다. 이는 압축률은 높이고, 정보 손실을 낮추려고 할 때 사용한다.
데이터를 전송하거나 저장할 때 compact 하게 할 수 있게 하는 방법론이다.
기계 학습에서는 data를 compact하게 만드는 경우가 자주 있다. 이는 보통 임베디드와 같이 환경이 제한된 경우에 속한다. compressed 된 data를 decode를 해야 하는데, 이때는 inverse function을 사용한다. 중요한 점은 decode시 distance가 굉장히 작아야 한다. 따라서 function을 잘 정의해야 한다.
정보 이론에서는 entropy라는 용어를 사용하는데 이는 다음과 같이 정의된다.
$$ \mathbb{H}(X) = -\sum_{k = 1}^{k}p(X = k) log_{2}p(X = k) $$
entropy가 최대인 경우는 $p$가 uniform distribution일 때다. 그 이유는 결과적으로 $X$에 대한 realization이 어디서 이루 어질지를 찾기가 힘들다. 이는 불확실성이 높아지기 때문이다. (확률이 어디서든 같으면 특정 feature가 있는 부분을 찾기 힘들다.)
가장 낮은 경우는 델타 함수를 띌 때이다. 결과적으로 $x$라는 위치에서 sample이 발생하기 때문이다.
$p(x) = \frac{1}{k}$ 라고 가정하면 $\mathbb{H}(x)$ 는 다음과 같아진다.
$$ \mathbb{H}(x) = \sum_{k=1}^{k}\frac{1}{k}log_{2}(\frac{1}{k}) $$
$$ = log_{2}k $$
Binary entropy
$X \in {0,1}, \ p(X = 1) = \theta, \ p(X=0) = 1- \theta$ 일 때 $\mathbb{H}(X)$는 다음과 같다.
$$ \mathbb{H}(X) = -\sum^{k}{k=1}p(X=k)log{2}p(X=k) \\= -[p(X=1)log_{2}p(X=1)+p(X=0)log_{2}p(X=0) \\ = -[\theta log_{2}\theta + (1-\theta)log_{2}(1-\theta)]: Binary \ Entropy $$
Kullback-Leibler (KL) Divergence
KL Divergence는 엔트로피를 조금 확장한 개념인데 조금은 다르다. KL divergence는 2개의 확률 분포에 대해 불확실성을 측정할 때 사용한다. 기존 엔트로피는 1개의 확률 분포에 대해 진행했다.
정확한 형태를 모르는 확률 분포 $p(x)$가 있다고 해보자. 그리고 이 확률 분포를 최대한 근사한 $q(x)$가 있다고 하자. 그럼 당연히 데이터의 실 분포는 $p(x)$이고, 우리가 예측한 분포는 $q(x)$라고 생각할 수 있다. 그리고 해당 데이터를 $q(x)$의 ecoding으로 전송한다고 해보자. 이때 $p(x)$와 $q(x)$의 정보량은 다를 수 있다. 이렇기 때문에 추가적으로 필요한 정보량의 기대값이 필요한데, 이를 KL divergence로 정의할 수 있다.
KL divergence 값이 크면 2개의 분포가 다르다는 의미이다. 반대로 작으면 두 분포가 유사하다는 의미이다.
정의는 다음과 같다.
$$ \mathbb{KL}(p \mid \mid q) = \sum_{k=1}^{k}p_{k}\log{\frac{p_{k}}{q_{k}}} = \mathbb{H}(p_{k})+\mathbb{H}(p_{k}, q_{k}) $$
비교적 엔트로피식이랑 비슷하다. 식을 조금 더 풀어쓰면 다음과 같다.
$$ \sum_{k=1}^{k}p_{k}\log{\frac{p_{k}}{q_{k}}} = \sum_{k=1}^{k}p_{k}\log(p_{k}) - \sum_{k=1}^{k}p_{k}\log(q_{k}) $$
$\mathbb{H}(p_{k}, q_{k})$는 cross entropy다. 어떤 데이터에 대한 분포가 p일 때, 이를 모델링 할 때 다른 모델 q를 가지고 이를 나타내는데 필요한 비트 수 이다.
$\mathbb{H}(p_{k}, q_{k}) = -\sum_{k=1}^{k}p_{k}\log(q_{k})$
$\mathbb{H}(p_{k}, p_{k}) = \mathbb{H}(p)$ 는 expect number of bit라고 한다. 의미는 우리가 true model을 사용한다고 가정할 때 예측하는 bit 수이다.
KL divergence는 데이터를 encode하는데 필요한 extar bit의 평균 size이고, 이는 distribution $p$ 대신 distribution $q$를 사용하여 데이터를 encode 했기 때문이다.
Extra number of bits는 $\mathbb{KL}(p \mid \mid q) ≥ 0$를 명확하게 해야하고, KL divergence는 오직 $p = q$일 경우에 성립한다.
$\mathbb{KL}(p \mid \mid q)$는 항상 0보다 크거나 작고, 0일 때는 $p$와 $q$가 같다.
Convex function
$\mathbb{KL}(p \mid \mid q) ≥ 0$이라는 조건을 증명하려면 convex function에 대한 개념을 알아야 한다.
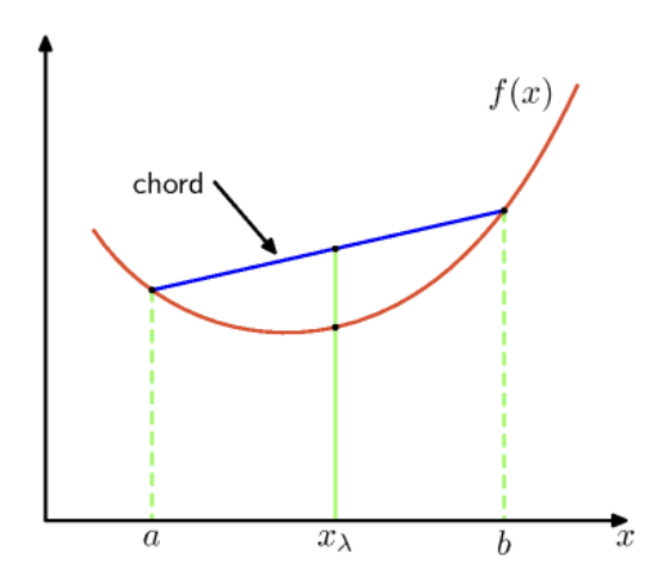
convex function을 한국어로 번역하면 볼록 함수이다. 어떠한 함수 $f(x)$에 대해 임의의 두 점 사이 chord (빨간 선)가 $f(x)$와 같거나 혹은 더 위쪽으로 형성된다면 이를 convex라고 한다.
이를 식으로 표현하기 위해, 임의의 구간 $a, b$를 정하고, 그 사이의 임의의 지점 $x_{\lambda} = \lambda a +(1-\lambda)b$로 정의할 수 있다. 이를 convexity를 구하는 수식으로 정리하면 다음과 같다.
$$ f(\lambda a + (1-\lambda)b) ≤ \lambda f(a) + (1- \lambda) f(b) $$
위 수식을 만족하는 함수를 convex function이라고 정의한다.
$f(x)$가 convex이면, $-f(x)$는 concave가 된다.
Jensen’s Inequality
convex function은 옌센 부등식이 성립한다. 수식은 다음과 같다.
$$ f(\sum_{i = 1}^{M}{\lambda_{i}x_{i}}) ≤ \sum_{i = 1}^{M}{\lambda_{i}f(x_{i})} $$
여기서 모든 $x_{i}$의 집합에 대해 $\lambda_{i} ≥ 0$ 이고, $\sum_{i}\lambda_{i} = 1$을 만족한다.
다시 KL divergence로 넘어와서 왜 0보다 크거나 같은지 증명해보자.
$$ -\mathbb{KL}(p \mid \mid q) = \sum_{k=1}^{k}p(x)\log{\frac{q_(x)}{p(x)}} \\ \leq \log{\sum_{x \in A}p(x)\frac{q(x)}{p(x)}} \ (\text{by} \ \text{Jensen's Inequality}) \\ = \log{\sum_{x \in A}{q(x)} \leq log \sum_{x \in X} q(x)} = 0 $$
2번째 term에서 옌센 부등식이 성립하는 이유는 log function이 concave function이기 때문에 성립한다. convave function의 경우에는 우리가 앞서 살펴본 옌센 부등식과 반대 부등식이 성립한다.
$p(x)$와 $q(x)$가 같은 경우에는 log function이 0이 된다.
Discrete distribution에서 entropy의 최대 값은 uniform distribution이다.
Uniform distribution을 함수로 표현하면 다음과 같다 . $u(x) = \frac{1}{\chi}$
이를 활용하여 KL divergence에 넣으면 다음과 같다.
$$ 0 ≤ \mathbb{KL}(p \mid \mid u) = \sum_{x}{p(x)\log \frac{p(x)}{u(x)}} \\
=\sum_{x}{p(x)\log{p(x)}} - \sum_{x}{p(x) \log{u(x)}} \\ =-\mathbb{H}(X) + \log(\mid \chi\mid) $$
이를 priciple of insufficient reason이라고 부르고, 모델링을 하고 싶을때 불확실 성을 KL divergence로 측정할 수 있고, $q$에 대한 분포를 잘 모를때 uniform 분포를 이용해 계산할 수 있다는 의미이다.
중요한 점은 모르는 분포에 대해 아무 분포나 $q$로 두는 것보다는 uniform 분포를 사용하면 해당 값 범위 내에서 수렴하기 때문에 비교적 수월하다는 점이다.
Mutual Information (MI)
Mutual information은 지난 convariance에서 잠깐 언급을 했었다. Coreelation은 어떠한 $\text{R.V.} \ x, y$의 관계를 알고 싶을 때 이용하였는데, 이는 연속형 변수에 한정되어 있고 선형적인 특성으로 정의된다는 문제점이 있다. 따라서 이를 보완한 이론이 Mutual Information (MI)이다. 우리는 joint distribution을 알고 있으면 두 개의 $\text{R. V.}$의 관계를 알 수 있다.
MI의 수식은 다음과 같다.
$$ \mathbb{I}(X; Y) = \mathbb{KL}(p(X, Y) \mid \mid p(X)p(Y)) \\ =\sum_{x} \sum_{y}p(x,y) \log{\frac{p(x,y)}{p(x)p(y)}} $$
MI의 수식을 수학적으로 해석하면 Marginal distribution을 가지고 얼마나 $x, y$가 matching이 잘되었는지를 KL divergence를 통해 구한다는 의미이다.
MI도 KL의 특성에 따라 항상 0보다 같거나 크다.
MI에서는 $p(x, y) = p(x)(y)$일 때 0이 된다. 이 말은 $p(x), p(y)$는 독립이라는 말이다.
MI를 entropy로 변환하여 수식을 정리하면 다음과 같다. (KL의 entropy 정의 사용)
$$ \mathbb{I}(X;Y) = \mathbb{H}(X) - \mathbb{H}(X \mid Y) = \mathbb{H}(Y) - \mathbb{H}(Y \mid X) $$
위 수식에서 $\mathbb{H}(Y \mid X)$ 는 conditional entropy라고 부르며 풀어서 쓰면 수식은 다음과 같다.
$$ \mathbb{H}(Y \mid X) = \sum_{x}p(x)\mathbb{H}(Y \mid X=x) $$
위 수식을 이용해 우리는 $X$와 $Y$ 사이의 MI를 $Y$를 observing 한 후 $X$에 대한 불확실성의 감소 또는 $X$를 observing한 후 Y에 대한 불확실성의 감소로 해석할 수 있다.
MI와 밀접한 관련이 있는 pointwise mutual information (PMI)는 기존 모든 사건에 대한 entropy를 평균화 할 때 주로 사용하는 MI와는 다르게 단일 사건에 대한 entropy를 측정할 때 사용한다.
수식은 아래와 같다.
$$ \text{PMI}(x, y) = \log{\frac{p(x,y)}{p(x)p(y)}} = \log{\frac{p(x \mid y)}{p(x)}} = \log{\frac{p(y \mid x)}{p(y)}} $$
위에서 언급한 것과 마찬가지로 PMI 수식에 대해 expectation을 구하면 MI가 된다.
Continuous $\text{R.V.}$에 대한 MI는 변수들을 sampling과 quantizing 과정을 거쳐 히스토그램으로 만든다. 여기서 sampling은 $x$ 범위 값을 나누어서 pointing을 하는 과정이고, quantizing은 이에 대한 역함수를 통해 $y$ 값을 정하는 과정이다. 이 과정을 통해 Continuous $\text{R.V.}$ 를 Discrete $\text{R.V.}$로 변환한다. 변환 과정에서 100% 변환은 하지 못하고 오차가 생겨 결과가 달라질 수 있다. 이렇게 변환한 변수에 대해 MI를 적용시킨 것이 MIC이다.
MIC에 대한 수식은 다음과 같다.
$$m(x,y) =\frac{\max_{G \in g(x,y)}{\mathbb{I}(X(G); Y(G))}}{\log{\min{(x,y)}}}$$
위 수식에서 $G$는 $X$와 $Y$ 값을 각 bin으로 나눈 2d grid이고, MI 함수 안에 있는 $X, Y$ 는 grid에 들어가는 distribution이다. 그리고 분모는 $X$ 방향 grid의 개수와 $Y$ 방향 grid의 개수 중 최소값을 의미한다. 이를 $\log$ 를 통해 normalization 함으로써 MIC 값이 0과 1 사이로 제한된다.
MI vs Correlation

위 그림을 살펴보면 MIC와 correlation이 모두 낮은 C 지점에서는 데이터 간 아무런 관계가 없는 모습이 보인다. 이는 C 지점에서 relation이 작다고 해석이 된다. H와 D 지점에서는 둘 다 linear relation을 띄는 모습을 볼 수 있고, E, F, G 지점에서는 corerelation이 발견하지 못하는 non-linear relationship을 MIC는 잘 catch 한 모습을 볼 수 있다.




