| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 서포트벡터머신이란
- DeepLearning
- CNN
- cnn 역사
- 논문분석
- EfficientNet
- SVM hard margin
- pytorch project
- RCNN
- yolo
- Deep Learning
- svdd
- Object Detection
- SVM margin
- libtorch
- TCP
- cs231n lecture5
- SVM 이란
- Computer Vision
- fast r-cnn
- pytorch
- yolov3
- darknet
- self-supervision
- computervision
- CS231n
- 데이터 전처리
- pytorch c++
- Faster R-CNN
- support vector machine 리뷰
- Today
- Total
아롱이 탐험대
Machine learning overview 본문
기계 학습의 유형
(1) Supervised learning
: Supervised learning이란 기계가 데이터와 이에 대한 label을 가지고 학습하는 방법론이다.
Train dataset: $D = {(x_{i}, y_{i})}^{N}_{i=1}$
이 식을 해석해보면 $x_{i}$ 는 학습 데이터 셋에 있는 $i$ 번째 데이터 feature를 의미하고 $y_{i}$ 는 $x$ 에 mapping 되는 label을 의미한다.
쉽게 설명하면 강아지 이미지가 $x$ 에 해당되고, 이에 대한 label 값인 강아지가 $y$에 속한다.
Supervised learning의 목적은 input data인 $x$ 를 output data인 $y$ 에 mapping 하는 방법을 배우는 것이다.
Input data $x_{i}$는 D 차원으로 이루어진 feature vector이고, 위 예시와 같이 이미지, 문장, 단어 등등이 될 수 있다.
output data $y_{i}$는 정답에 해당하는 label이기 때문에 무엇이든 될 수 있다. classification과 같이 분류 문제에서는 label을 주로 class라고 부른다. 이를 수식으로 표현하면 다음과 같다. $y_{i}=\left\{ 1, \cdots , C \right\}$
label은 또한 regression과 같은 회귀 문제에서는 real-value가 될 수 있다.
Classification
Classification은 supervised learning의 가장 대표적인 예이다. classifiaction의 목표는 input $x$ 로부터 ouput $y$ 를 mapping 하는 것을 기계가 학습하는 것이다.
정답 label인 $y$ 는 위에서 살펴본 supervised learning의 설명과 마찬가지로 $y_{i}=\left\{1, \cdots , C\right\}$ 로구성된다. 여기서 만약 $C$ 의 개수가 2개 라면 bianary classification이 되고, 2개 이상이면 multiclass classification이라고 부른다. 만약 데이터 셋 $x$ 에 대해 정답 label $y$ 가 여러 개 존재하는 경우에는 multiple related binary class label이라고 부른다. 이는 만약 label이 {모자, 고양이, 강아지}가 존재하고 dataset이 모자를 쓰고 있는 고양이라면 이에 대한 정답 label이 {모자, 고양이}가 되는 경우와 같다.

보통 classification problem이라고 하면 multiclass classification이라고 생각하면 된다.
classification을 단순한 수식으로 표현하면 $y=f(x)$ 라고 봐도 무방하다. 여기서 $f$ 는 알려지지 않은 함수이고, 우리의 학습 목표는 $D = {(x_{i}, y_{i})}^{N}_{i=1}$ 를 가지고 함수 $f$ 를 추정은 것이다. 그 후 우리는 새로운 input인 $x$ 를 가지고 $\hat {y}=\hat {f}(x)$ 로 예측할 수 있다. 여기서 hat symbol은 예측 값이라는 의미이다.
Probablilistic classification
input vector인 $x$ 와 학습 데이터 셋 $D$ 가 주어졌을 때, 우리는 $p(y\mid x, D)$ 를 통해 각 label에 대한 예측 확률을 얻을 수 있다. 예를 들면 class가 2개만 존제하는 binary classication의 경우 $p(y= 1\mid x, D)$ 와 $p(y=2\mid x, D)$ 를 각각 구해 2개의 label에 해당하는 예측 확률 값을 얻을 수 있다. 물론 $p(y= 1\mid x, D) + p(y=2\mid x, D) = 1$ 일 것이다.
만약 제작한 model이 여러개라면 $p(y \mid x, D, M)$으로도 표현할 수 있다.
여기서 궁금한 점은 기계 학습에서 확률이라는 개념은 왜 필요할까? 단순히 train dataset 만 가지고 기계 학습의 모든 flow를 커버할 수는 없다. train dataset 은 한정되어 있고, model은 다양한 상황에 대해 설계가 되어야 된다. 이때 model의 학습 능력이 잘되어가고 있는지에 대한 불확실성이 생기게 되고, 이러한 불확실성을 평가하기 가장 좋은 도구가 확률적 접근이다. 어떠한 label을 예측한다고 할 때 $p(y \mid x, D)$을 통해 해당 모델이 얼마나 신뢰도 있게 학습을 했는지 확률로써 표현할 수 있다.
MAP(maximum a posteriori) estimate
한국어로는 최대 사후 확률이라고 부르고, 이는 사후 확률의 최빈값을 의미한다. 그렇게 어렵지 않은 개념이다.
$\hat{y}=\hat{f}(x)= argmax^{c}_{c=1} p(y=c \mid x, D)$
수식의 의미는 학습 데이터 셋 $D$와 input dataset $x$가 주어지고 class가 1인 경우에 이를 최대화하는 model을 찾는다는 뜻이다.
Regression
regression은 연속적인 실수 값 $x$, $y$에 대해 model을 fitting하는 것을 목표로 두는 방법론이다. fitting model은 선형적일 수도 있고, 비선형적일 수도 있다. 현실에서는 넷플릭스 추천 시스템과 같이 매우 높은 dimenstion이 있는 data일 수도 있고, outlier가 존재할 수도 있고, smooth하지 않은 data도 있어 굉장히 많은 방법론들이 존재한다.
(2) Unsupervised learning
: Unsupervised learning이란 기계가 데이터만을 가지고 특성을 학습하는 방법론이다.
Train dataset: $D = {(x_{i})}^{N}_{i=1}$
위 식은 Supervised learning과는 달리 학습 데이터는 오직 feature만 주어 진다.
실제 대부분의 상황에서 label이 주어지는 경우는 거의 없다. 따라서 현재 가장 대두적인 방법론이다. 기계는 데이터 셋 $D$ 에서 interesting 한 pattern을 찾아야 한다.
따라서 Unsupervised learning은 데이터 셋에 대한 density를 추정하는 문제로 생각할 수 있다.
Density estimation
위에서 언급한 바와 같이 실제 대부분의 상황해서는 label을 얻기 힘들기 때문에 unsupervised learning이 필요하다. Density estimation은 어떤 데이터의 분포를 학습하는 방법이고, $p(x_{i}\mid \theta)$를 통해 model을 제작하게 된다. 여기서 $\theta$의 의미는 model의 parameter이다. 수식을 해석하면 $\theta$에서의 $x_{i}$의 분포를 예측하는 것이고 이는 Supervised learning의 $p(y_{i} \mid x_{i}, \theta)$와는 전혀 다른 의미이다.
그 외의 다양한 기법들
clustering
clustering이란 각 featrue에 해당하는 clutter의 대한 분산을 예측하는 것이다.
2차원 좌표에 data feature를 mapping한 후 오른쪽과 같이 이를 같은 특성을 같은 class로 군집화하는 것이 clustering이다. 이를 수식으로 표현하면 다음과 같다.
$K* = argmax_{K}{P(K \mid D)}$
이는 dataset $D$를 통해 $K$번째 cluster에 속하는 최대의 확률을 구하는 수식이다. 이를 통해 각 data를 가장 높은 확률로 예측한 cluster로 분류를 한다. 이 과정을 통해 각 data point $i$를 각 cluster $z_{i} \in \left\{1, \cdots, k\right\}$에 mapping 한다. 그 후 새로운 data가 들어오게 되면 유사한 feature를 갖고 있는 cluster로 분류한다.
$z*{i} = argmax{k}P(z_{i}=k \mid x_{i}, D)$
Dimenstionality reduction
Chapter 1-1) Dimensionality Reduction Overview
해당 포스트 글에 자세히 설명되어있다.
Graph structure
edge와 node를 사용해 가장 관련된 다른 node와 edge를 통해 연결되어 있는 model 구조이다.
Matrix completion
conv pooling 과 비슷하게 행렬 내 정의되어 있지 않은 element에 대해 추측하는 방법론
Parametric Models
Model을 parameter 관점에서 분류할 수 있다. parametric model이란 model이 가지고 있는 parameter들이 미리 정의되어있는 상태에서 fixed parameter를 가지고 학습을 하는 것을 의미한다.
parametric model의 장점은 빠르게 동작하며, 구현 난이도가 비교적 쉽다. 하지만 data distribution 자체에 대해 정확하게 추정할 수 있는 알고리즘으로 설계가 되어야 한다.
ex) Linear regression, logistic regression SVM...
Non-Parametric Models
Non-parametric model은 주어진 dataset $D$에 대해 학습하는 model이다. parameter의 수는 train dataset의 양에 따라 가변적이다. 이 때문에 parametric model에 비해 model이 flexible 하다.
하지만 큰 data가 증가하면 train 및 test, inference의 복잡도가 parametric에 비해 상대적으로 증가되고, modeling 난이도 또한 더 어렵다. 또한 dataset의 distribution에 대한 가정 없이 주어진 data만을 가지고 최적의 model을 구하는 방법으로 parameter의 개수도 바뀔 수 있다.
Non-parametric model의 예시로 K-nearest neighbor에 대해 알아보자.
K-nearest neighbor (KNN)
traing set에서 주어진 test input $x$와 가장 가까운 $K$개의 point를 본다고 가정하자. KNN은 이때 test input인 $x$가 어떤 class에 속할지를 예측하는 문제이다.
여기서 $K$는 우리가 직접 선택해야 하는 hyperparameter이다.
식은 다음과 같다.
$$p(y = c | x, D, K) = \frac{1}{K} \sum_{i \in N_k (x,D)}{I(y_i = c)}\\
I(e) =
\begin{cases}
1, & \quad if\ e\ is\ true \\
0, & \quad otherwise
\end{cases}$$
$N_{k}(x, D)$는 $x$에 대한 K nearest point의 indices이다.
수식을 해석해보면, $x$가 어느 class에 속하는지 확률적으로 구할 수 있게 된다. 예를 들어 $K=4$인 class의 분포에 대해 어떤 점 $x$에 대한 KNN을 구하게 되면 $\frac {1}{4} \sum_{i \in N_k(x, D)} I(y_i = c)$에서 점 $x$에 대한 4개의 nearest point에 대해 $I(y_i = c)$을 구해 4로 나누면 된다.
정리하면 KNN 알고리즘은 parameter를 학습하는 것이 아니라, 주변 data의 분포를 통해 prediction을 진행하는 것으로 볼 수 있다.
예를 들어 설명하자면 K가 4이고, label은 {사과, 바나나}라고 하자. input data point $x$에 대해 가장 인접한 4개의 data를 비교한다. 만약 가장 인접한 데이터 4개 중 3개가 사과, 1개가 바나나라고 하면 위 수식을 통해 사과는 3/4, 바나나는 1/4이기 때문에 최종적으로 input data $x$는 사과라고 판별하게 된다.
KNN classifier의 경우 굉장히 알고리즘적으로 심플하고, 유클라디안이나 L2 distance와 같이 좋은 distance가 주어지면 잘 작동한다.
하지만 KNN의 성능은 feature dimenstion의 증가에 따라 상당히 저하된다. 이러한 문제를 curse of dimensionality라고 부른다.
input data가 D-dimensional 단위로 균일하게 분포되어 있을 때, KNN Classifier를 적용하는 상황을 고려해보자. data point의 원하는 비율 $f$까지 test point $x$ 주변에 hyper-cube를 증가시켜 class label의 density를 추정한다고 가정하자. 그렇다면 기대되는 cube의 edge length 값은 $e_{D} = f^{\frac {1}{D}}$라고 할 수 있다.
만약 $D = 10$이고, density class label의 estimation이 data의 10%에 근거한다면, 기대되는 edge length는 다음과 같다.
$e_{10}(0.1) = 0.1^{0.1} \approx 0.8$
여기서 data의 1%만 사용했다면 식은 다음과 같이 변한다.
$e_{10}(0.01) = 00.1^{0.1} \approx 0.63$
이러한 KNN의 curse of dimensionality를 아래 그림을 통해 다시 보자.

왼쪽 그림에서 작은 정육면체인 small cube의 길이를 s라고 하고, large cube를 l이라고 하면 number of dimension의 함수로 unit cube를 커버하는데 필요한 cube의 edge 길이를 오른쪽 그래프처럼 표현할 수 있다
이를 통해 알 수 있는 사실은 feature에 대한 dimension이 커짐에 따라 KNN classifier가 cover 해야 할 data 수가 점점 많아진다. 이는 Nearest neighbor에 대한 data만을 가지고 decision을 하지 못하고, 더욱 넓은 범위의 data를 통해 decision을 해야 함을 의미하며, KNN classifier가 올바르게 동작하지 못하게 된다. 따라서 KNN은 feature dimension이 작은 경우에는 유용하지만, dimension이 큰 경우 model의 complexity가 높아지고, 이에 따라 성능이 낮아진다는 결론을 얻을 수 있다.
Parametric models
이러한 Curse of dimensionality의 해결책이 parametric model이다.
parametric model은 data의 분포를 추정한다. 앞서 설명한 Supervised learning, Unsupervised learning 유형에 따라 다음과 같이 수식을 정의한다.
$p(y \mid x)$: Supervised learning
$p(x)$: Unsupervised learning
이러한 추정은 inductive bias라고 부를 수 있고, 이는 parametric model의 형태로 자주 표현된다.
Linear regression
parametric model의 대표적인 예로 Linear regression에 대해 살펴보자.
Linear regression은 response는 input들의 linear function이다. 이를 토대로 linear regression의 function은 다음과 같다.
$y(x) = w^T{x} + \varepsilon = \sum^D_{j=1}w_jx_j + \varepsilon$
여기서 $x$는 input feature vector, $w$는 weight vector라고 할 때, $w^T{x}$는 $w^{T}$와 $x$의 scalar 곱이고, $\varepsilon$는 linear prediction과 실제 response 간의 residual error를 의미한다.
이러한 residual error는 실질적 추정에서는 Gaussian 또는 normal distribution으로 modeling 한다.
Linear regression을 수행할 때, response는 어떤 input x에 대한 linear function이라고 가정할 수 있다. 여기서 학습해야 할 parameter는 weight이다.
이러한 linear regression을 확률적으로 표현하면 다음과 같다.
$p(y | {x}, \theta) = N(y | \mu({x}), \sigma({x}))$
위 수식을 Gaussian distribution과 어떻게 연결 지을 수 있을까?
다음과 같이 assumption을 만들면 된다.
- the mean is Linear function, $\mu = w^Tx$
- noise fixed, $\sigma^2(x) = \sigma^2$
- parameter of this model is $\mu = (w, \sigma^2)$
결국 linear regression은 Gaussian 확률 모델을 이용하여 표현할 수 있는데, mean을 Gaussian으로 표현할 수 있는 Normal distribution ($\varepsilon \sim N(\mu, \sigma^2)$)으로 가정했다. 그렇기 때문에 Gaussian model의 property에 의해 $\mu = w^Tx$ 이고, $\sigma^2(x) = \sigma^2$ 이므로, 이 model의 parameter는 $w$ 와 $\sigma^2$으로 표현할 수 있다.
만약 input이 1차원이라면 $\mu(x) = w_0 + w_1x = w^Tx$로 표현할 수 있고, input vector x는 다음과 같이 $x = (1, x)$로 표현할 수 있다. 여기서 1은 dummy vector이다.
Basis function expansion
앞서 linear regression을 linear product로 표현했는데, x를 어떤 non-linear function으로 바꿈으로 인해 linear regression을 non-linear relationship model로 만들 수 있다.
$p(y | x, \theta) = N(y | w^T\varphi(x), \sigma^2)$
위 수식을 보면 앞에서 $\mu = w^Tx$처럼 바로 $x$ 를 $w^T$와 linear production 했던 것과 다르게, non-linear function $\varphi(x)$을 통해 non-linear 형태로 사용한다.
대표적으로 다음과 같은 polynormial regression을 사용한다.
polynomial regression : $\varphi(x) = [1, x, x^2, ... , x^d]$
linear 함수와는 다르게 polynomial regression을 사용하면 굉장히 flexable 한 형태로 사용이 가능하다.
Logistic regression
logistic regression은 linear regression을 classification에 일반화하는 것에 초점을 둔다. 기존 $y$에 대한 가우시안 분포를 $y \in \left\{0,1\right\}$를 따르는 베르누이 분포로 교체함으로써 classification에 특화된 regression으로 만든다. 이는 기존 연속적인 값인 $y$를 discrete한 값으로 바꿨다는 의미이다.
베르누이 분포를 설명하기 전 베르누이 시행에 대해 알아야한다. 이는 결과가 두 가지 중 하나로만 나오는 실험이나 시행을 뜻한다. 베르누이 시행의 결과를 실수 0 또는 1로 바꾼 것을 베르누이 확률 변수라고 한다. 베르누이 확률 변수는 두 값 중 하나만 가질 수 있으므로 이산확률변수이다. 베르누이 확률 변수의 분포를 베르누이 분포라고 부른다.
베르누이 분포에 대한 수식은 다음과 같다.
$$p(y \mid x, w) = Ber(y \mid \mu(x))$$
(1) $$\mu(x) = E[y \mid {x}] = p(y = 1 \mid {x})$$
(2) $$0 ≤ \mu(x) ≤ 1$$
$\mu(x)$의 의미는 두 가지 시행 중 1이 나올 확률을 의미한다. 이는 모수 (parameter)라고 부른다.
우리는 $\mu(x)$의 범위를 0~1에 해당하는 값으로 바꾸어줘야한다. 이를 보장하기 위해 sigmoid function을 사용한다.
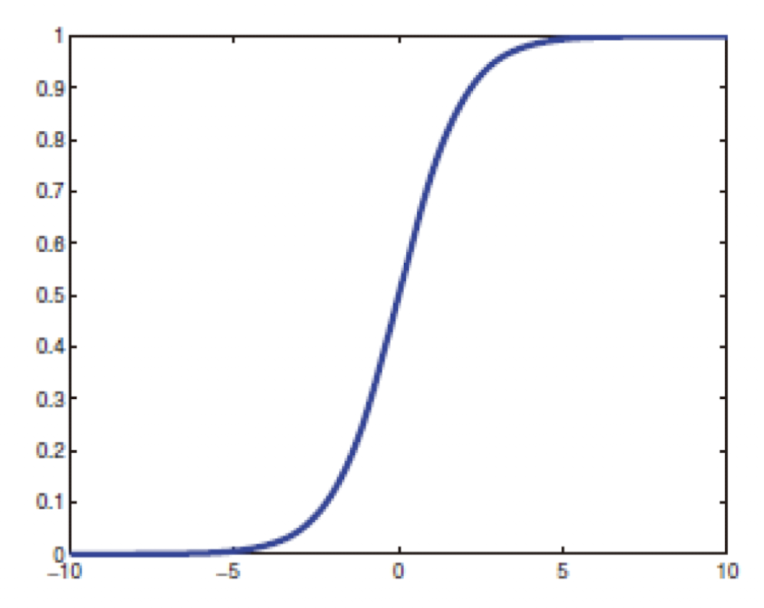
sigmoid에 대한 수식 정의는 다음과 같다.
$$\mu(x) = sigm(w^{T}X)$$
$$sigm(\eta) = \frac{1}{1+exp(-\eta)} = \frac{e^{\eta}}{e^{\eta + 1}}$$
위 수식과 그래프를 보면 알겠지만 sigmoid function은 output의 boundary를 0과 1사이로 제한할 수 있다.
따라서 위 베르누이 분포에 대한 수식에 sigmoid 함수를 적용하면 다음과 같다.
$$p(y \mid x, w) = Ber(y \mid sigm(w^Tx))$$
수식을 더욱 간소화시키면 다음과 같다.
$$p(y_{i} \mid x_{i}, w) = sigm(w^{T}x_{i})=sigm(w_{0}+w_{1}x_{i})$$
threshold를 0.5로 설정해 최종적인 output을 결정한다. 0.5로 정하는 이유는 sigmoid 함수의 범우가 0부터 1사이기 때문이다.
여기서 decision rule이 어떤 train set에 대해 non-zero error rate를 가질 수 있냐는 물음을 가질 수 있는데, 다음 그림을 통해 살펴보자.

위 그림에서 초록색 점은 같은 x축에 위치하지만 다른 label 값을 갖는 모습을 볼 수 있다. 이를 통해 logistic regression을 이용해서 완벽하게 sampling 할 수 없다는 점을 보여준다.
logistic regression과 linear regression은 굉장히 유사한데, 이는 sigmoid function을 사용한 것을 제외하고는 둘 다 유사한 함수 형태로 표현되기 때문이다.
Overfitting
overfitting은 model을 학습함에 있어 만들어진 function이 지나치게 train data에 딱 들어 맞는 다는 것을 의미한다. 이 경우는 train data에 대한 모든 noise까지 function이 학습했기 때문에 나타나는 결과다. 이러한 noise까지 model이 fitting하게 되면 train data에 대해서는 error rate가 작지만, 실제 test 환경에서는 좋은 성능을 작지 못한다.
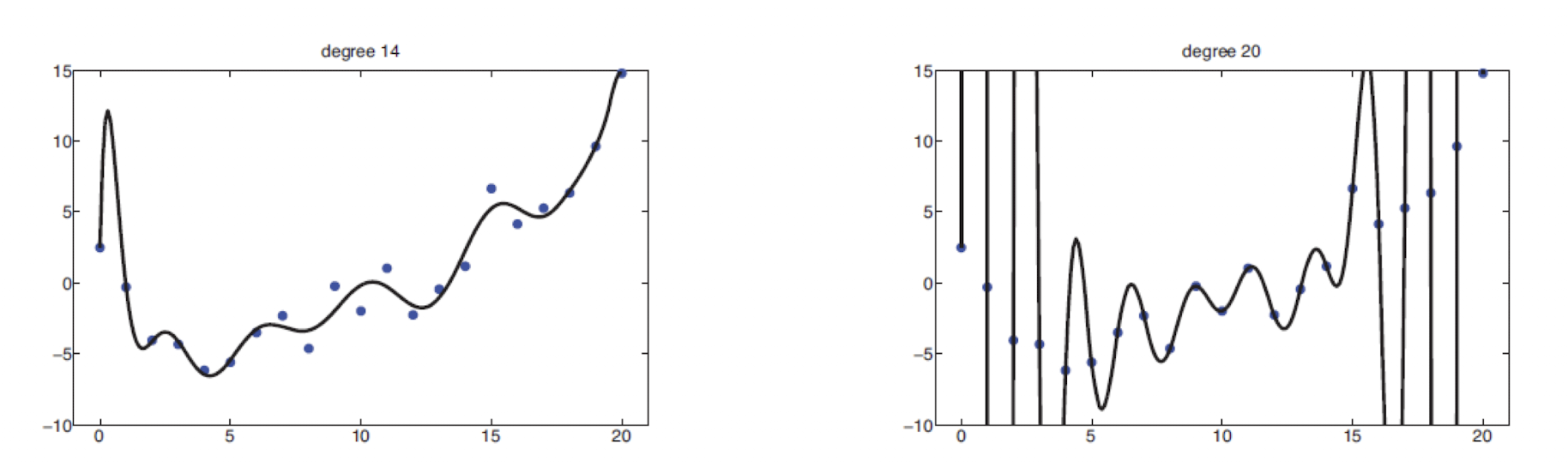
이는 high degree polynomial이 오른쪽과 같이 extreme oscilliation을 갖는 곡선을 생성하게 된다. 그 결과로 예측하려는 데이터에 대해 부정확한 추론이 나오게 된다.
앞서 설명한 KNN에서의 overfitting case에 대해 살펴보자. KNN은 K의 개수마다 model의 복잡도가 달라진다. K가 작은 경우에 overfitting이 잘 발생한다. 그 이유는 K가 작을 수록 주변에 있는 데이터들을 잘 안본다는 의미이기 때문이다. 따라서 아래 그림과 같은 결과가 나오게 된다.

K=1인 경우에는 1개의 data에 대해서만 연산을 진행하기 때문에 error가 존재하지 않는 대신 매우 짜글짜글한 것을 볼 수 있다.
K=5인 경우에는 더욱 smooth 해진 모습을 볼 수 있다.
만약 K=N이라면 가장 많은 label 값을 갖는 값으로 색이 변할 것이다. (모든 데이터를 고려하기 때문에)
Model selection
Classification의 경우 model selection을 위해 가장 보편적으로 사용하는 방법은 train dataset에 대해 misclassification rate를 계산하여 이를 가장 줄일 수 있는 model을 선택한다. 수학적으로는 다음과 같이 표현할 수 있다.
$$err(f, D) = \frac{1}{N}\sum^{(N)}{i=1} I(f(x_i) \neq y_i) = \frac{1}{N}\sum^{(N)}{i=1} I(\hat y_i \neq y_i)$$
$f$는 임의의 모델, $D$는 N개의 sample data를 갖는 train set이라고 할 때 misclassification rate는 모든 sample data에 대해 $I(f(x_i) \neq y_i)$한 값의 합에 $N$으로 나눈 값이 된다.
Generalization error
generalization error는 미래 데이터에 대한 misclassification rate의 평균 값이다. 이는 train set과는 독립인 test set에 대해 계산한다.
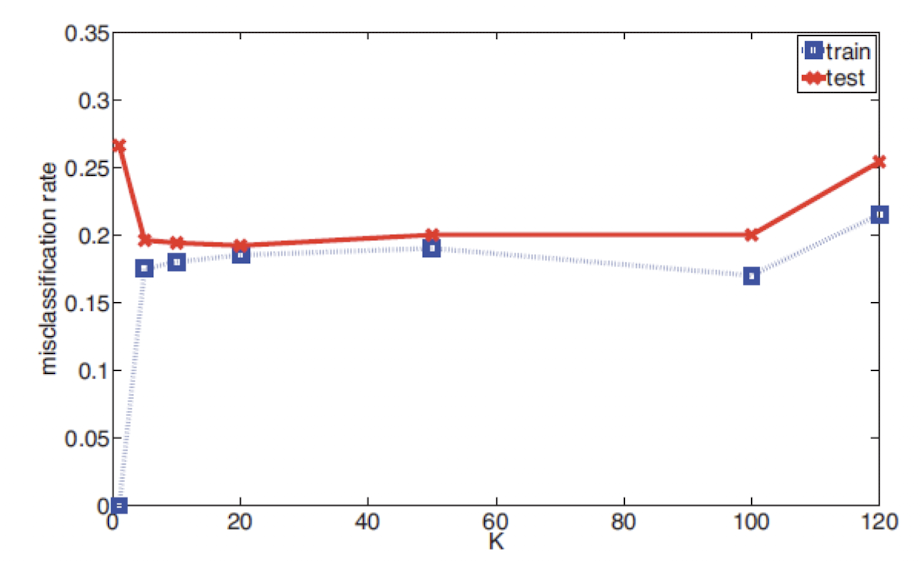
위 그림은 K 값에 따른 misclassification rate를 보여준다. K=1일 때 train error는 0이고, K 값이 커짐으로써 train error가 커지는 경향을 볼 수 있다. 하지만 실제로 중요한 것은 test error이다. 그리고 이 test error는 바로 generalization error를 의미한다. test error는 K 값이 증가함에 따라 줄어드는 경향을 볼 수 있다. K = 1일때는 높지만 train이 작은 경우를 overfitting이라고 부른다. 반대로 K = 120인 경우에는 train error도 높고 test error도 높다. 이를 underfitting이라고 한다. 말 그대로 model이 data에 대해 fitting이 덜 된 상황을 뜻한다. 10 ≤ K ≤ 100 부근에서는 제대로 학습된 것을 볼 수 있다.
Cross Validation
위 처럼 train, test error를 수월하게 측정하기 위해서는 충분한 데이터 셋이 필요하다. 하지만 만약 데이터 수가 부족한 경우에는 Cross validation을 사용하면 된다. 이는 training dataset을 K개의 fold로 나누어 K 번째 fold를 제외하고 나머지 fold에 대해 임의의 model $f$를 학습한다.
이렇게 하면 모든 데이터는 K번 만큼 train, test set을 만들 수 있다. 매 회차에서 K - 1개 fold를 train으로 사용하고, 1개의 fold를 test에서 사용한다.

만약 K = 5인 5-fold cross validation이라면 80%의 데이터를 train에 사용하고 20%의 데이터를 test에 사용한다. 위 그림과 같이 총 5번 만큼 iteration을 진행하고, 각 iteration마다 train, test set이 다르다. 그림에서 빨간 부분이 test fold이다.
만약 K = N인 경우를 LOOCV(Leave-One Out Cross Validation)이라고 한다. 이는 모든 data case에서 i 번째를 제외하여 model을 학습시키고, i번째 data에 대해 test를 진행한다.
이러한 방법 뿐만이 아니라 validation을 할 때 학습 데이터가 지나치게 적으면 model의 학습이 제대로 이루어지지 않아 over-underfitting이 될 가능성이 크다.
No Free Lunch Theorem = 범용적으로 사용할 수 있는 최고의 모델은 존재하지 않는다.




