| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- SVM margin
- SVM hard margin
- support vector machine 리뷰
- yolo
- pytorch project
- cnn 역사
- fast r-cnn
- libtorch
- computervision
- 서포트벡터머신이란
- Faster R-CNN
- EfficientNet
- Object Detection
- CS231n
- yolov3
- pytorch c++
- cs231n lecture5
- pytorch
- svdd
- TCP
- darknet
- SVM 이란
- 데이터 전처리
- 논문분석
- CNN
- DeepLearning
- Deep Learning
- Computer Vision
- RCNN
- self-supervision
- Today
- Total
아롱이 탐험대
Lecture 7: Convolutional Neural Networks 본문

지난 시간에 이어서 본격적으로 Convolutional Neural Networks에 대해 알아보자

CNN에서 합성곱 연산을 어떤 방식으로 하는지 보자.
우선 CNN에 들어오는 image의 size를 32*32*3이라고 가정하자. 여기서 32는 각각 weight와 height를 의미하고 3은 depth를 의미한다. 처음에 들어올 때는 RGB라고 생각해도 무관하다. 그리고 해당 Image를 filter라는 것을 통해 합성곱 연산을 해준다. 연산 과정은 뒤에서 설명하겠다. 위 예시에서는 5*5*3 size의 filter가 존재한다. 여기서 주의해야 할 점은 filter의 depth와 image의 depth는 같아야 한다.

위처럼 image와 filter를 통해 합성곱 연산 후 bias값을 더해주는 구조이다. filter는 맨 왼쪽 위부터 쭉쭉 순차적으로 훑으면서 합성곱 연산을 한다. 여기에서는 5*5*3번 총 75번 합성곱 연산을 해준다. (한 영역만 합성곱 연산을 했을 경우)

filtering 과정 후에는 각각 연산이 되어서 나온 layer를 activation map이라고 부른다.

만약 filter가 6개가 존재한다면 총 filtering 되어서 나오는 activation map의 개수는 6개가 된다.

대략적인 CNN의 구조를 보면 Input image가 filter를 통해 activation map을 만들고, 이 activation map은 다음 filter를 통해 또 다른 activation map을 생성하게 된다. 여기서 우리가 잘 설정해야 되는 부분은 filter의 값들이다.
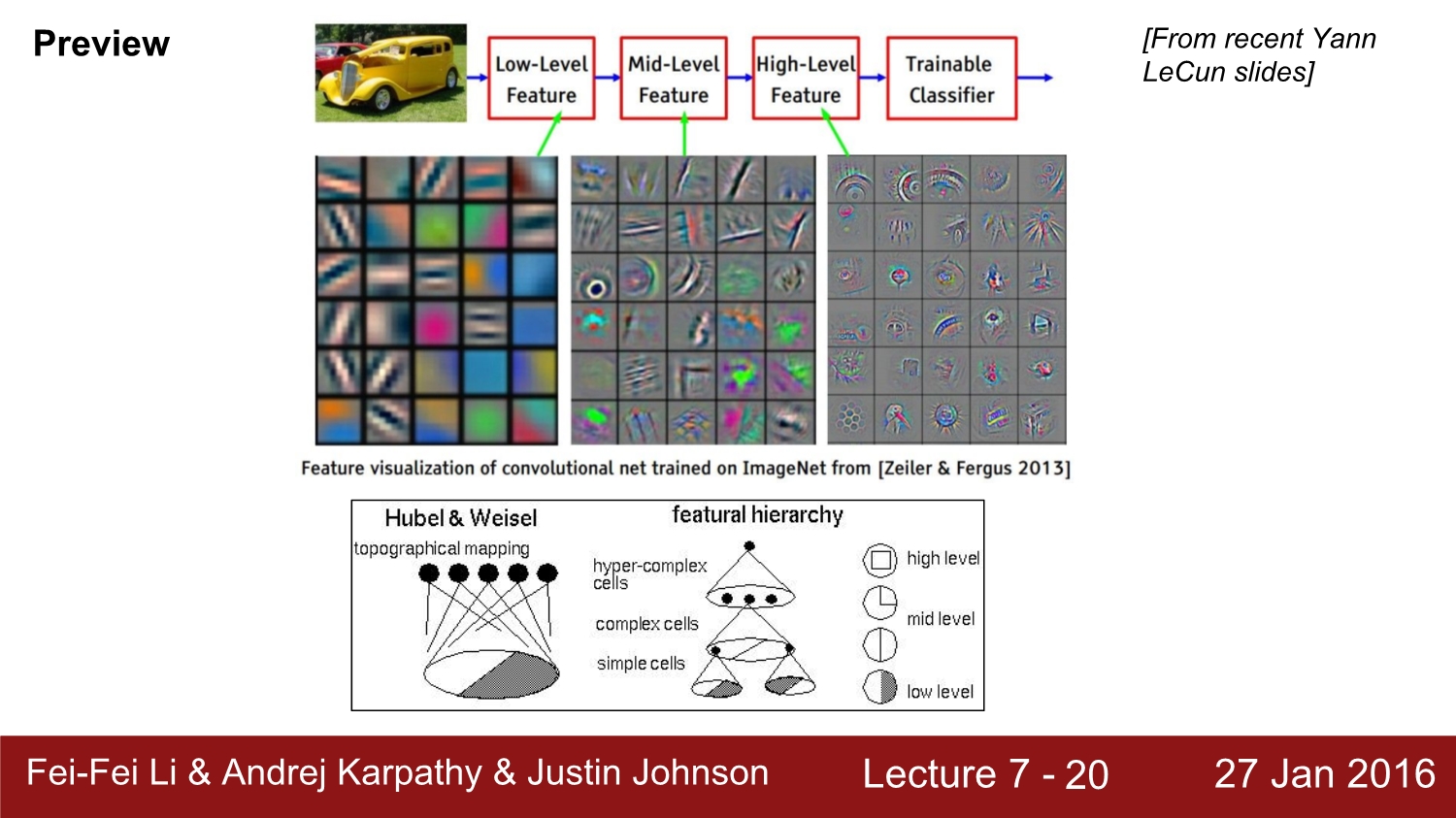
그러면 filtering 된 각각의 activation map은 어떤 식으로 되어있을까? low-level feature 즉 앞선 layer로부터 나온 activation map을 살펴보면 blob들이 보인다. 낮은 단계에서는 edge와 color 등이 관찰되고, 단계가 깊어질수록 조각들이 점점 통합되는 모습이 보인다. 깊은 레이어로 갈수록 상위 레벨의 이미지들을 관찰할 수 있다.
또한 이전 시간에 설명한 Hubel & Weisel이 생각한 구조와 cnn의 구조가 매우 유사하다고 한다.
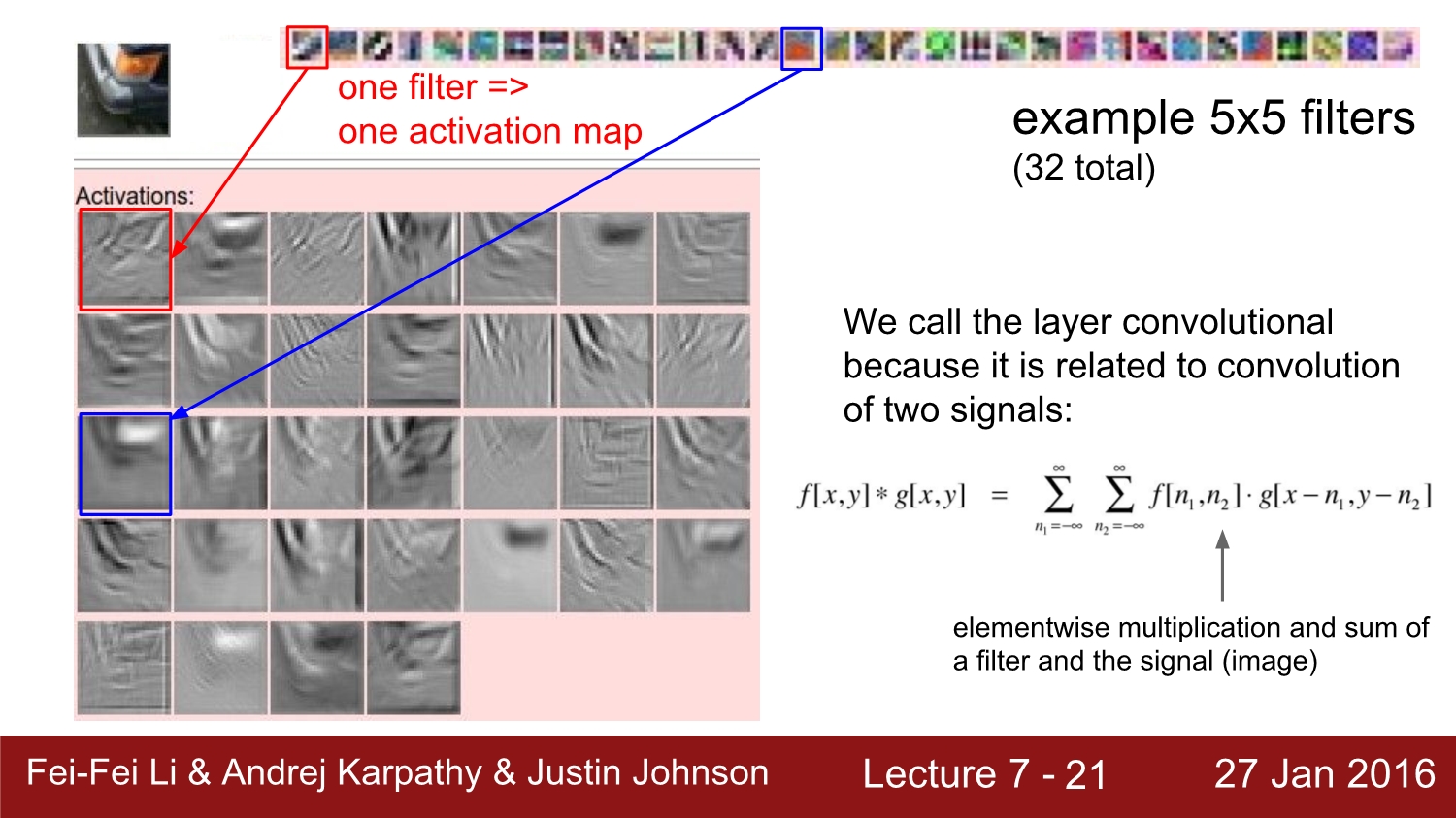
이것은 각 학습된 filter들이 어떤 모습을 하고 있는지에 대한 이미지이다. 각 필터에 대해 activation map이 생성되는데 색이 있는 부분과 비슷할수록 activation은 점점 하얘지는 모습을 볼 수 있다.
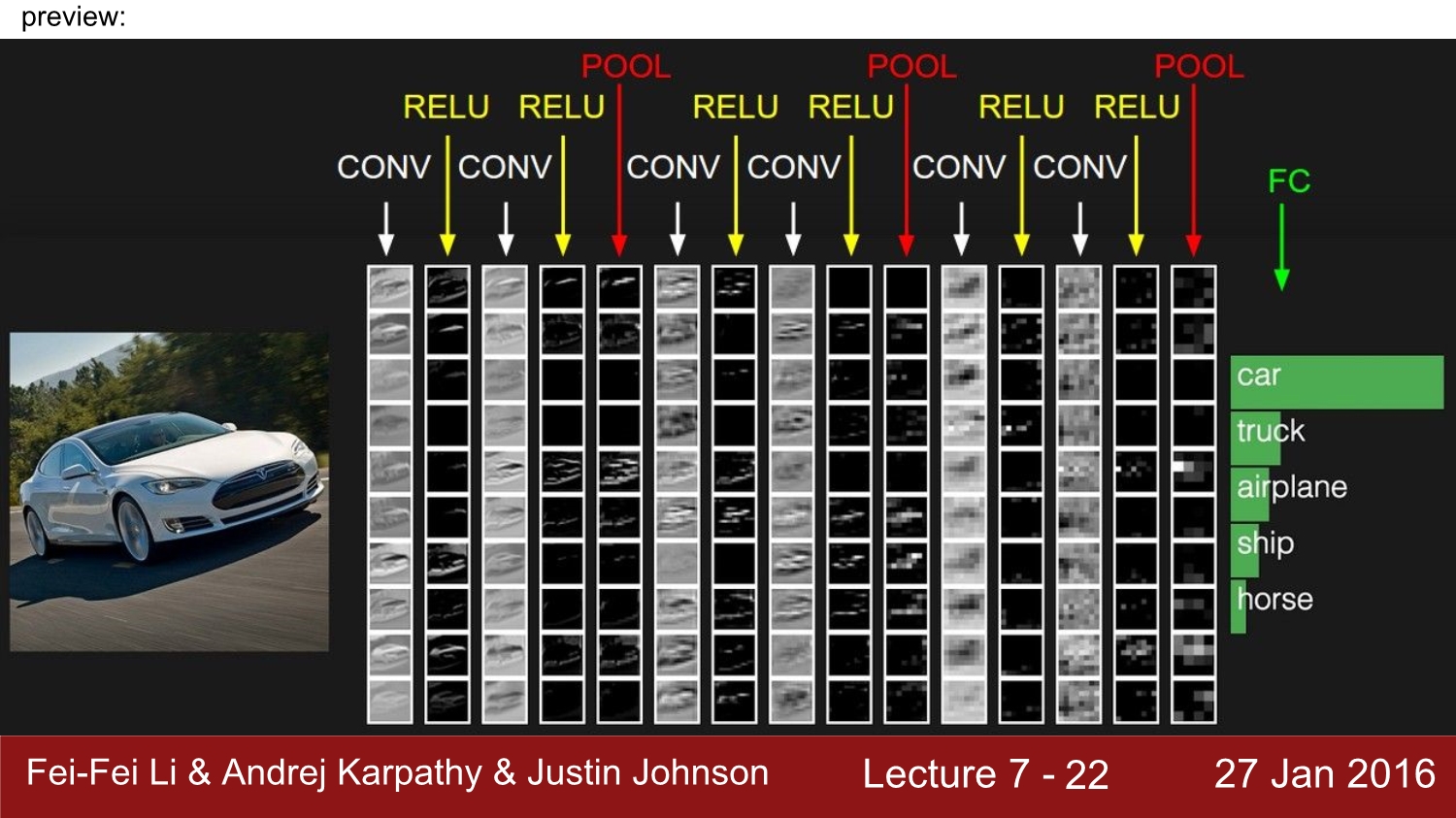
convolution과정과 pooling 과정을 거쳐서 나온 activation map들은 결국 맨 마지막에 FC(fully connected layer)를 통해 1*1*n의 사이즈로 나오게 되고 이를 softmax와 같은 loss function을 활용하여 각 class마다 score를 계산하게 된다. 위 예시는 자동차가 가장 확률이 높다고 할 수 있다.
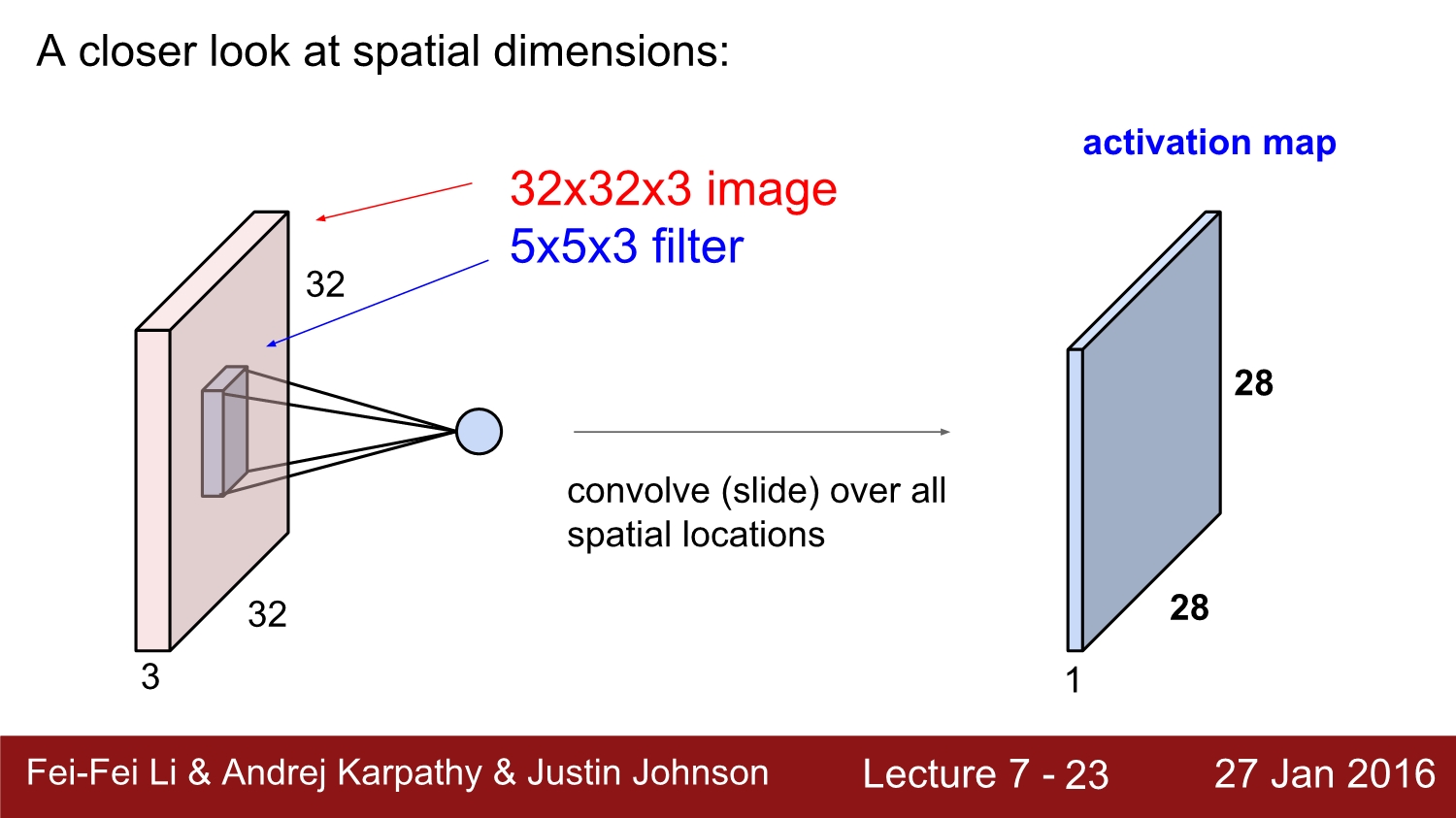
공간의 차원에 대해 한번 생각해보자. 과연 28이라는 숫자는 어떻게 나오게 되었을까?



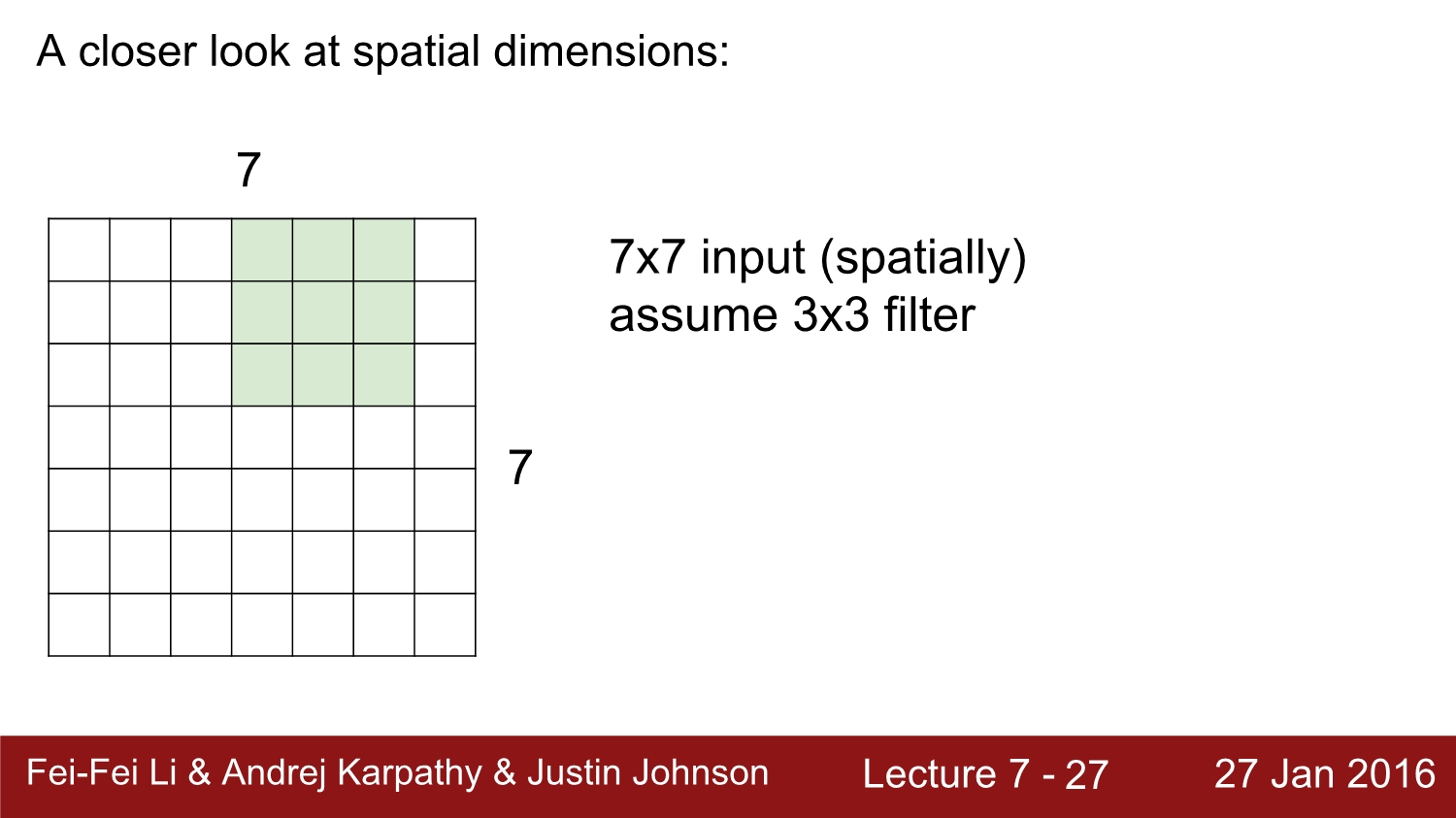
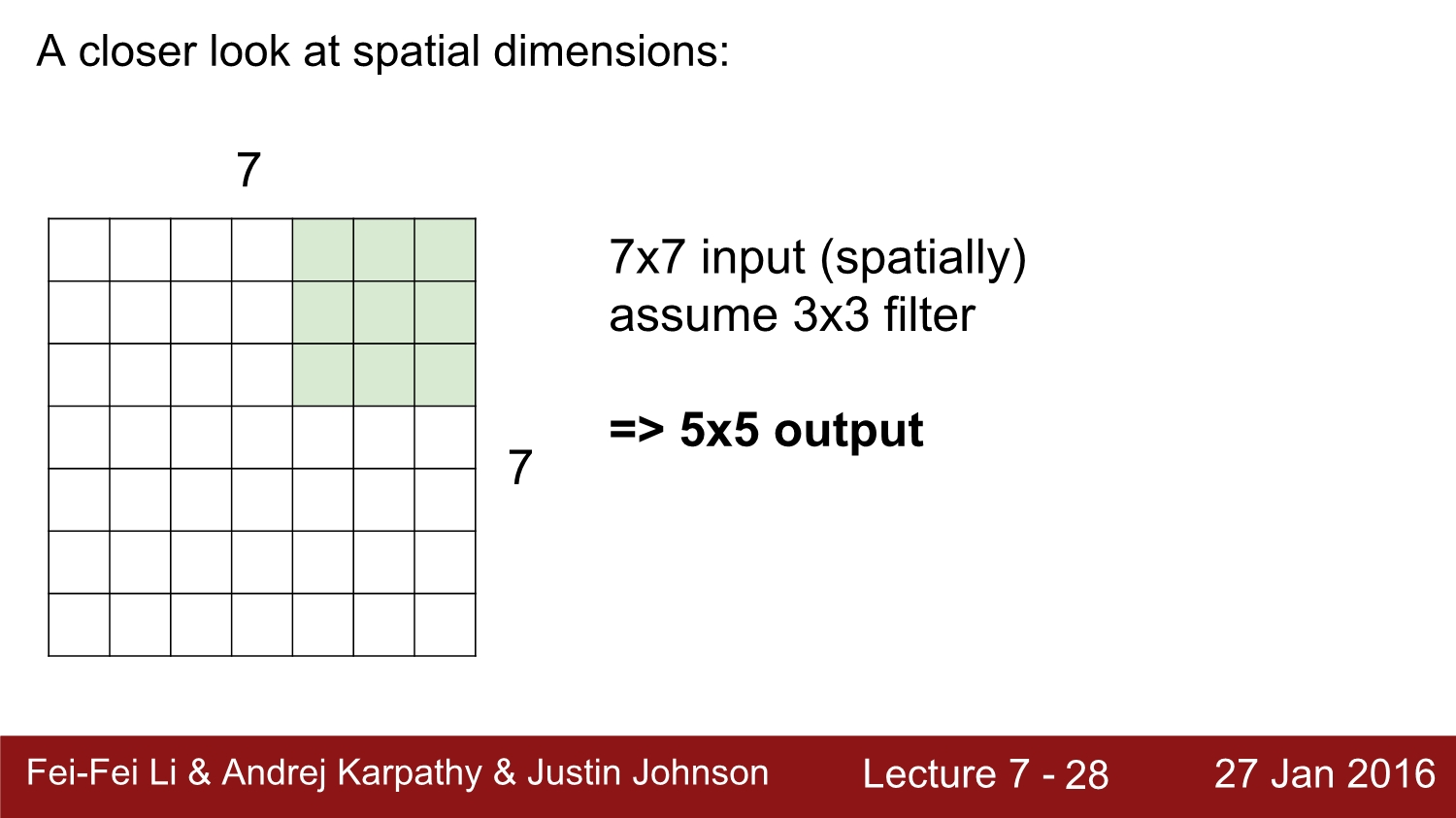
이와 같이 7*7 input에 3*3 filter를 적용시키면 총 1칸씩 5번 shift. 즉 5*5 output이 나오게 된다. 여기서 1칸씩 shift 하는 것을 stride가 1이라고 한다.

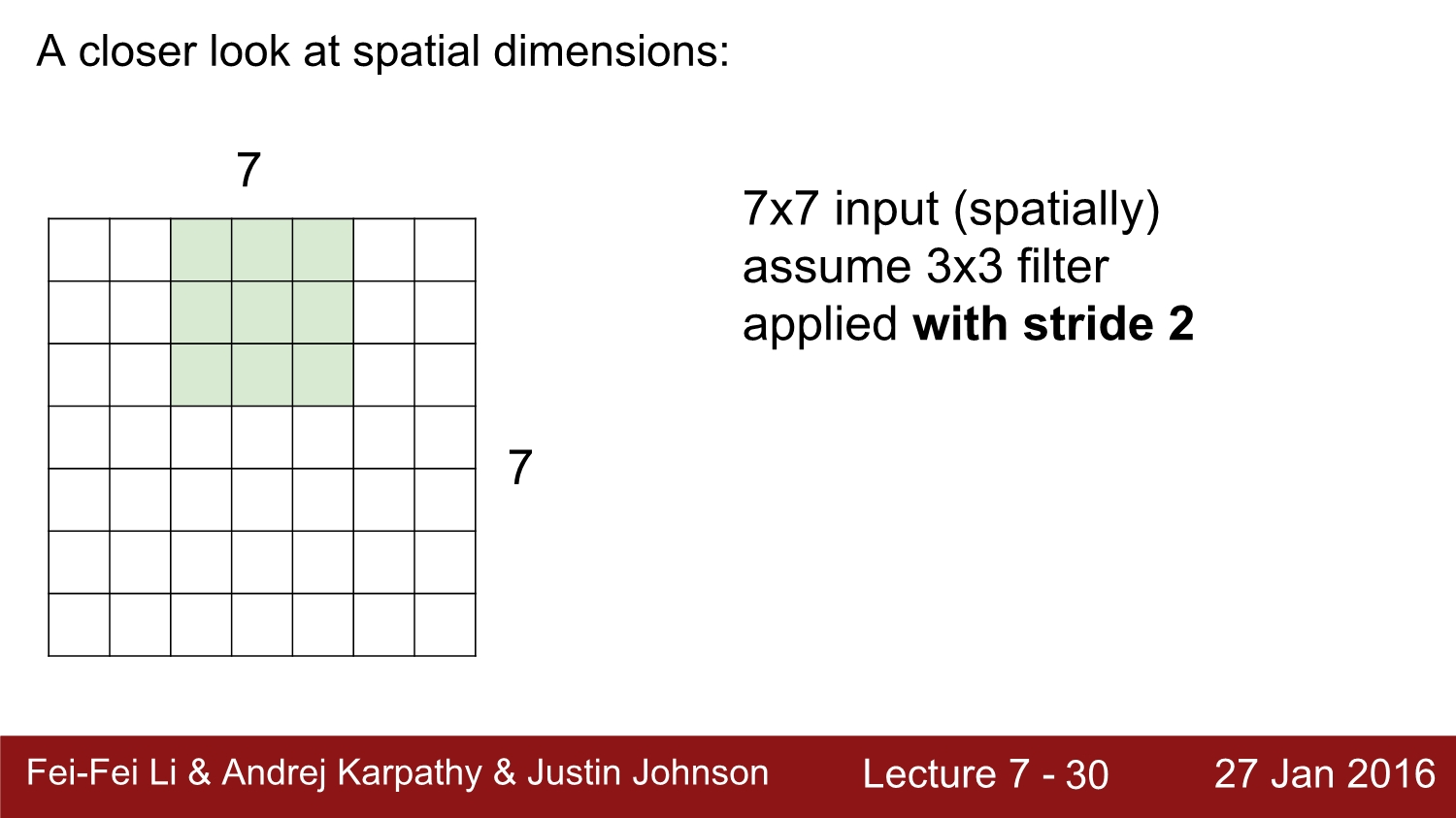

이것은 stride가 2일 때이다. output은 총 3*3이 나오게 된다.

stride가 3인 경우에는 fit 되지가 않는다.

output size의 식을 일반화하면 (N-F)/stride+1 이 된다. 원칙적으로는 정수가 아니면 사용하지 않는다.

filtering 과정을 계속 진행하게 된다면 어느 정도 이상부터는 크기가 매우 작아지기 마련이다. 크기가 작아지면 결국 나중에는 더 이상 convolution 연산을 할 수 없게 되는데, 이를 보완하고자 padding이라는 작업을 통해 activation map의 size를 보존시킨다. padding 방법은 여러 가지가 있지만 가장 많이 쓰이고 가장 단순한 0 padding에 대해 알아보자.
0 padding은 말 그대로 actvation map 테두리에 0을 추가함으로써 size를 보존하는 방법이다. 해당 ppt에서 질문이 만약 stride pad with 1 pixel을 하면 output이 어떻게 변화할까인데 정답은 7*7 size가 된다. 다시 한번 강조하지만 padding은 activation map의 size를 protect 하기 위해 사용한다. 그리고 padding으로 size를 보존하려면 (f-1)/2만큼 padding 처리를 해주면 된다.

예를 들어 input이 32*32*3, 10개의 5*5 filter가 stride 1, pad2로 convoltuon 하면 output의 size는 어떻게 될까?
정답은 위와 같이 (32+2*2-5)/1+1 = 32이고, filter의 개수가 10개임으로 최종적으로는 32*32*10이다.
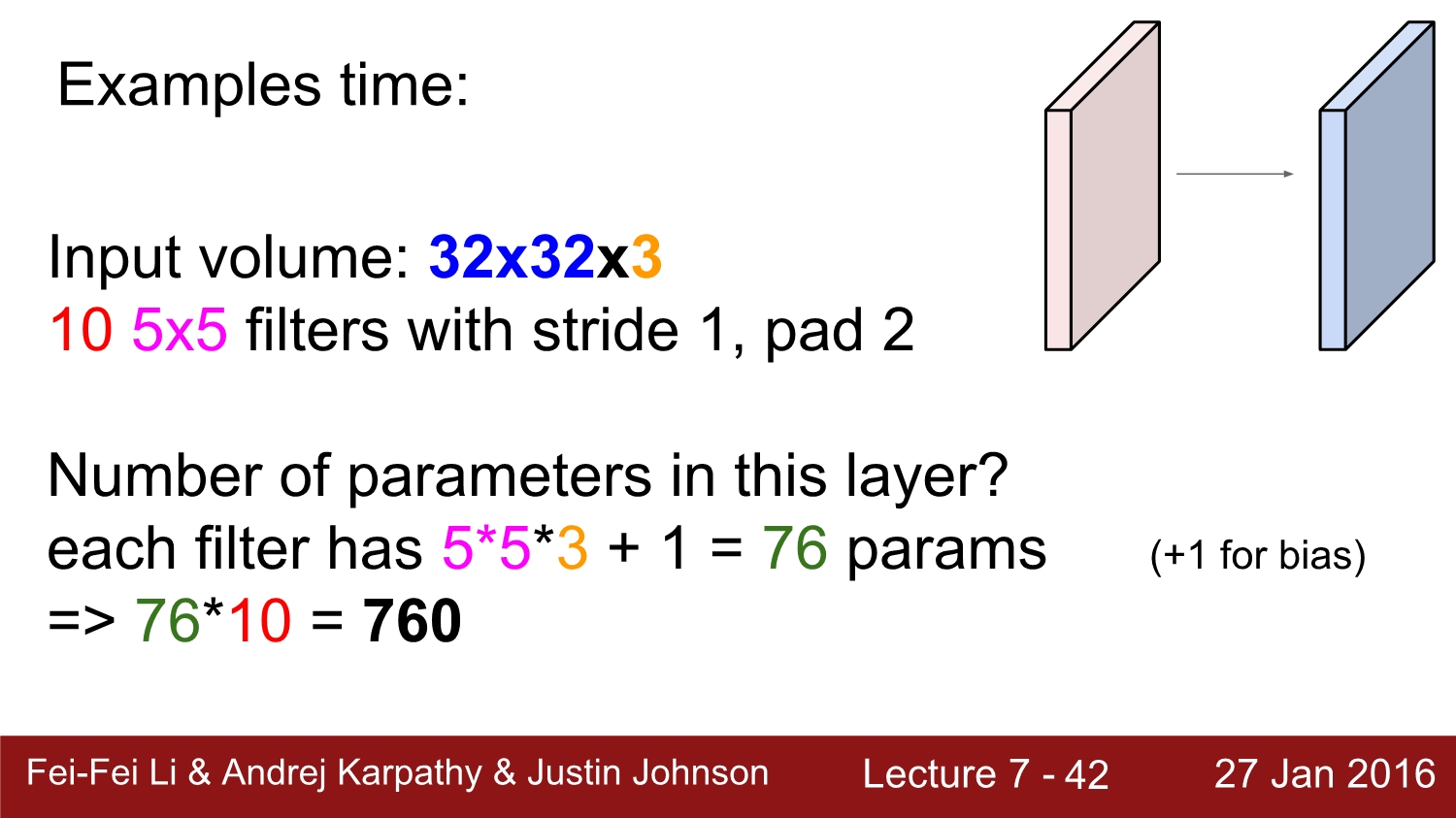
2번째 질문은 아까와 같은 조건일 때 parameter의 개수는?
정답은 필터의 크기인 5*5*3에 bias인 1을 더한 76이고 최종적으로는 filter가 10개임으로 76*10=760개가 된다.

지금 가지의 식들을 일반화하자면 위처럼 된다. 연산은 위에서 많이 연습했으니 생략한다.
보통 filter의 size는 2^n으로 한다고 한다. 이렇게 setting 할 경우에 performance 측면에서 훨씬 좋아진다고 한다.
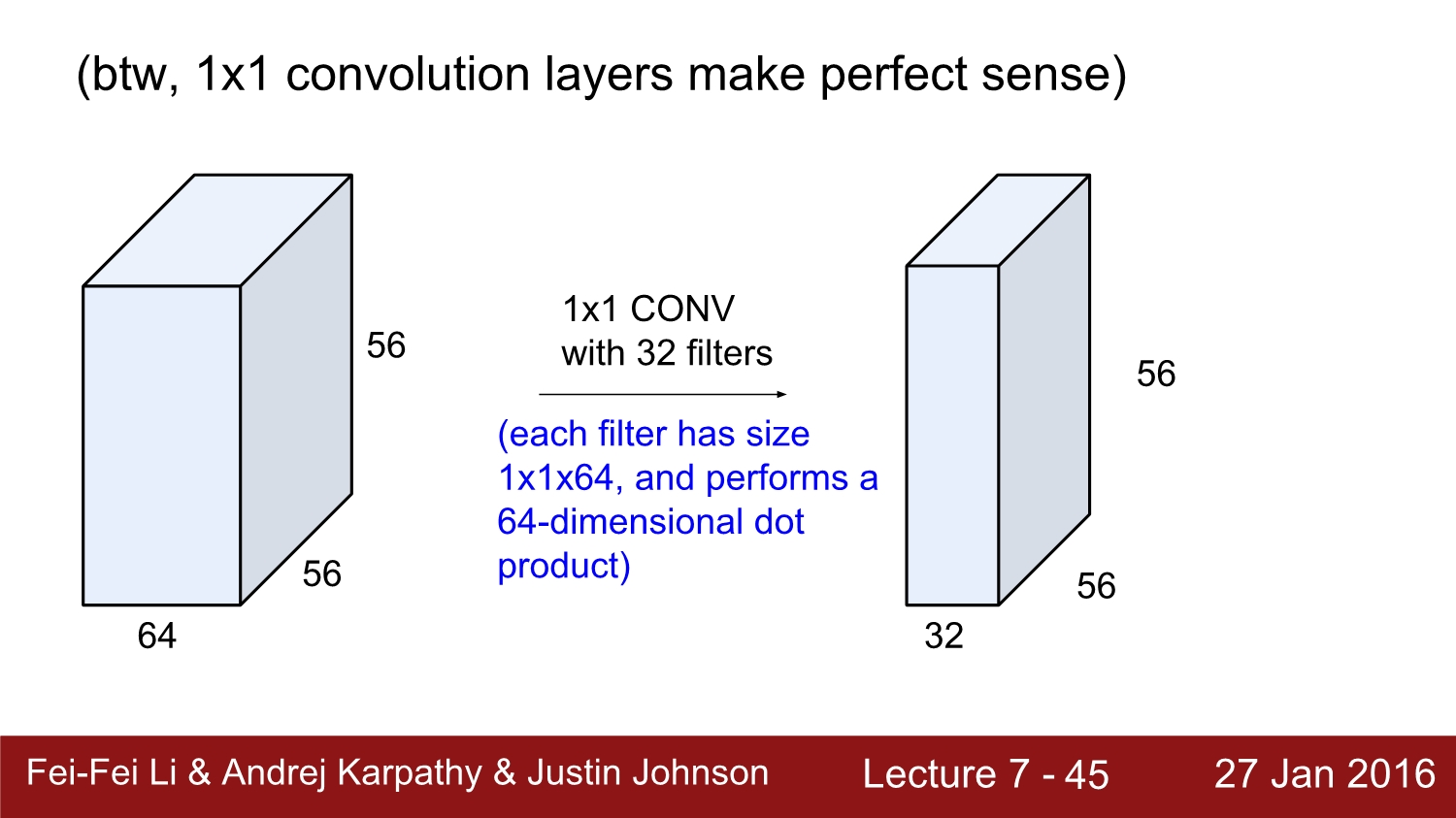
만약 filter의 size가 1*1일 경우에는 어떤 의미가 있을까? 만약 우리가 2차원에 대해서 계산을 한다고 하면 의미가 없게 되지만 3차원 공간에서는 각 filter를 통해 filtering 되면서 연산이 됨으로 의미가 있다고 한다.

뉴런의 관점으로 보면 convolution layer는 locality의 성질을 가지고 있다고 한다. 이를 보면 각각의 뉴런들이 동일한 parameter를 공유한다는 사실을 알 수 있다. 이를 parameter sharing이라고 한다.

각각의 activation map에서 동일한 위치에 있는 애들은 동일한 뉴런을 바라보고 있다. 하지만 그들 간의 서로의 weight를 공유하지 않는다. 그 이유는 각각 다른 depth에 속하기 때문이다.
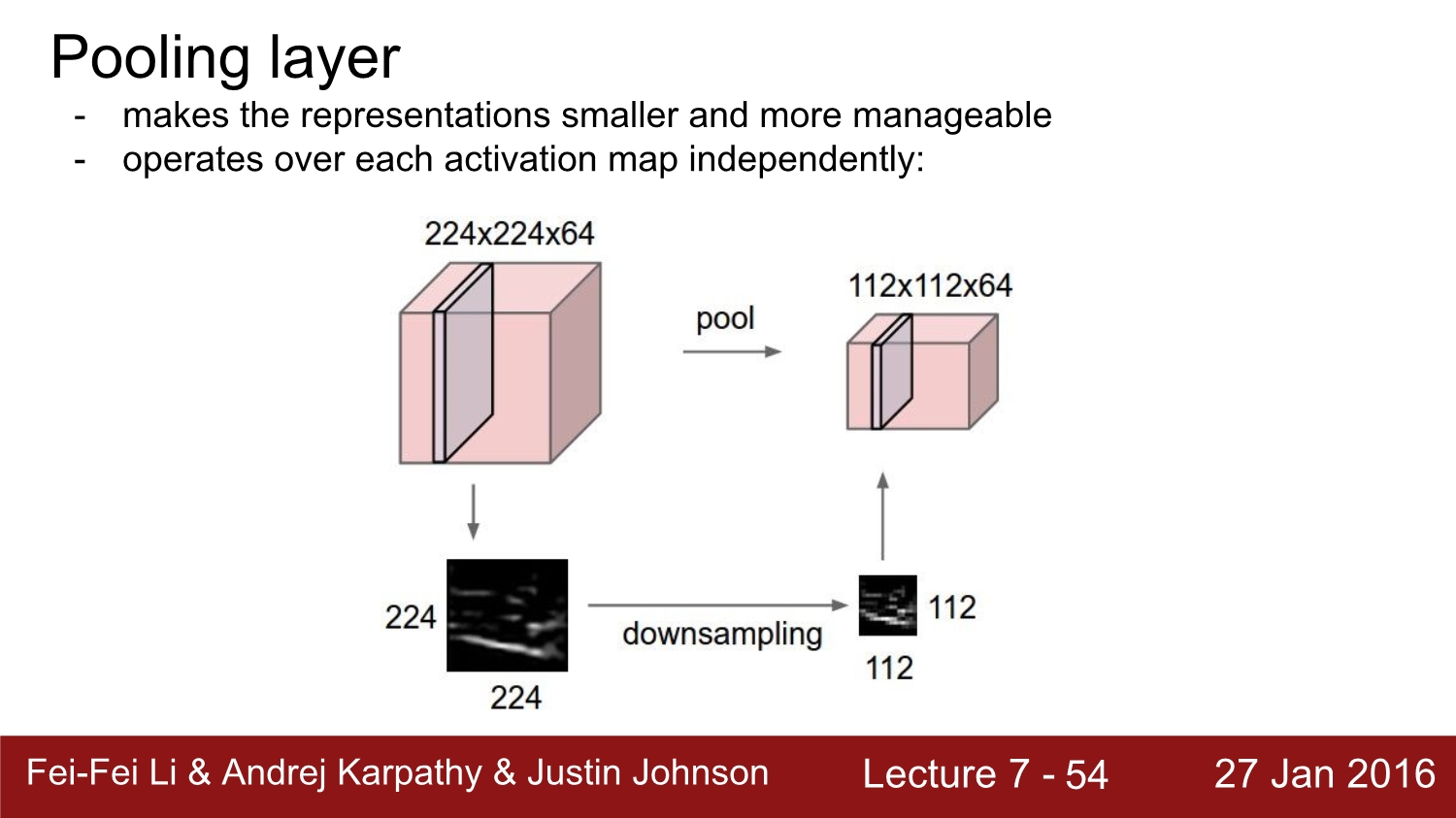
이번에는 pooling layer에 대해 알아보자. pooling layer는 각각의 activation map에 대해 독립적으로 작용한다. pooling layer는 depth를 유지하면서 downsampling을 시행한다. size에 관련된 일을 하는 layer는 pooling layer라고 생각하면 된다. pooling layer는 weight와 padding이 필요하지 않는다.
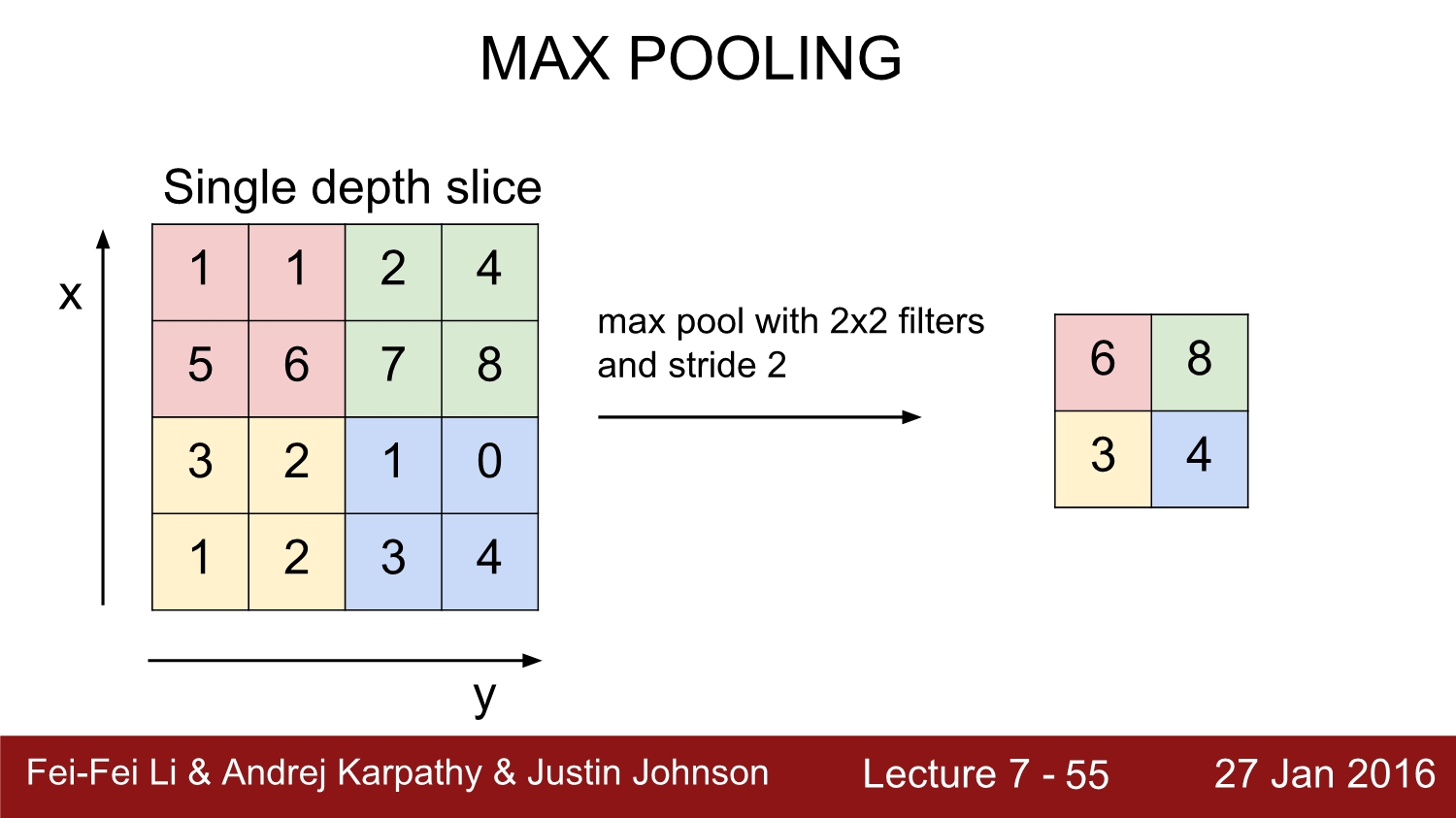
위에서 이해가 잘 안 되면 해당 이미지를 보면 바로 이해가 될 것이다. pooling에 대해서는 많은 기법이 있지만 여기서는 가장 많이 쓰이는 max pooling에 대해 설명한다. max pooling은 위에서는 2*2 filter와 2 stride를 기준으로 진행한다. 맨 왼쪽 2*2 size의 빨간색 상자를 보면 여기서 가장 큰 수는 6 임으로 6만 내버려두고 나머지를 다 없앤다.
size의 식을 일반화하면 (n-f)/s+1이다. 여기서 n은 input size, f는 filter size, s는 stride이다. max pooling을 진행하게 된다면 정보를 잃지 않을까?라는 궁금증이 있지만 이는 의도적으로 약간의 정보를 손실함으로써 invariance 함을 얻게 된다고 한다.
여기까지가 각 layer에 대한 설명이었고 다음은 현재까지 나왔던 유명한 model들에 대해 알아보자
간단하게 설명하고 자세한 건 내 블로그의 논문 리뷰 링크를 참고하면 된다.
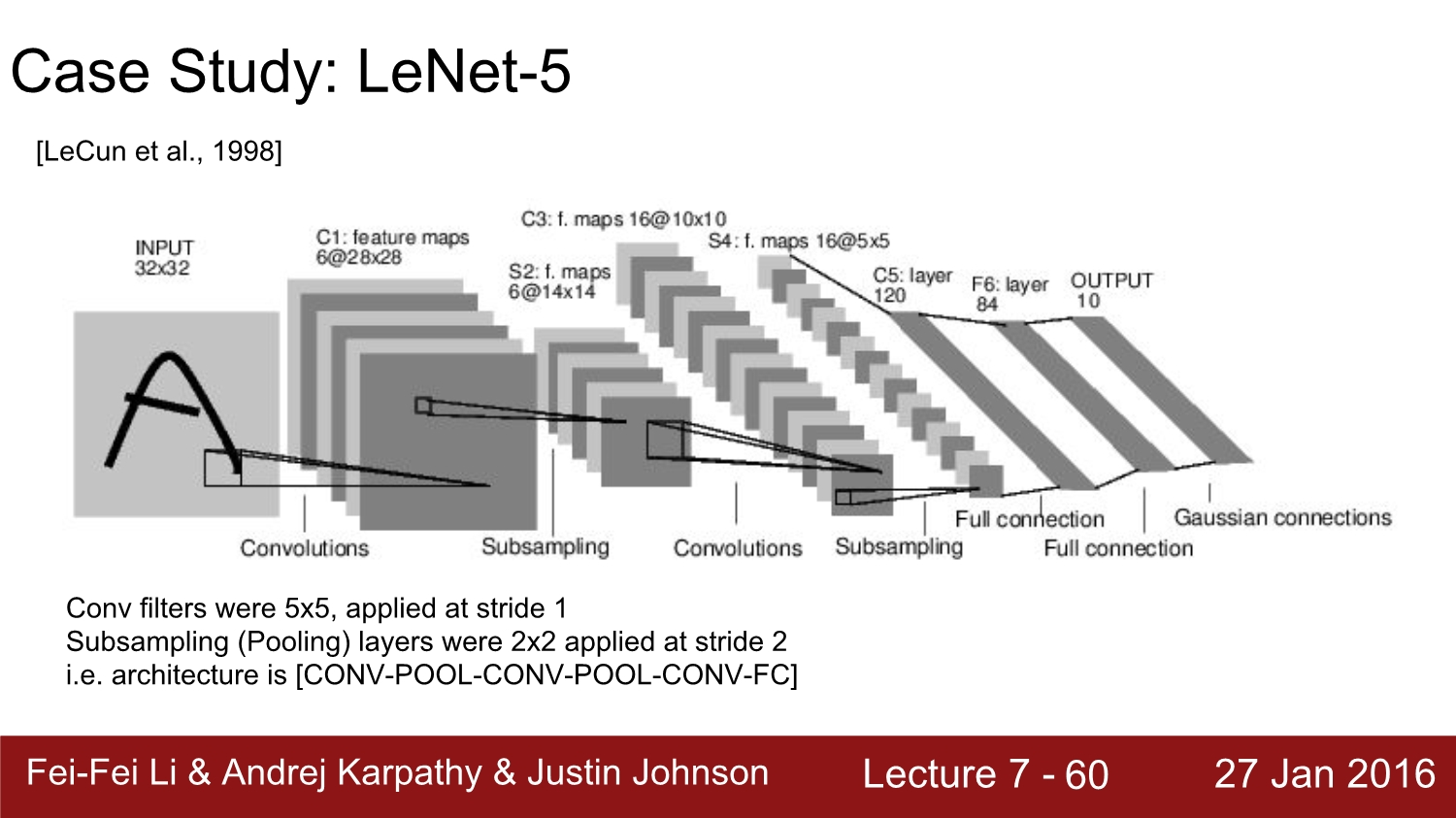
Le-Net: https://ys-cs17.tistory.com/2
Le Net - 5
Le Net - 5 -Yann LeCun- 1. Introduction - 본 네트워크의 원 논문 이름은 ‘Gradient-based learning applied to document recognition’이라고 한다. 1998년 CNN을 처음 개발한 Yann Lecum 연구팀이..
ys-cs17.tistory.com

Alex net: https://ys-cs17.tistory.com/3
ALEX Net: ImageNet Classification with Deep Convolutional Neural Network
ImageNet Classification with Deep Convolutional Neural Network (Alex Net) -Alex Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton- 1. Introduction Alex Net의 원래 이름은 ImageNet Classification with De..
ys-cs17.tistory.com
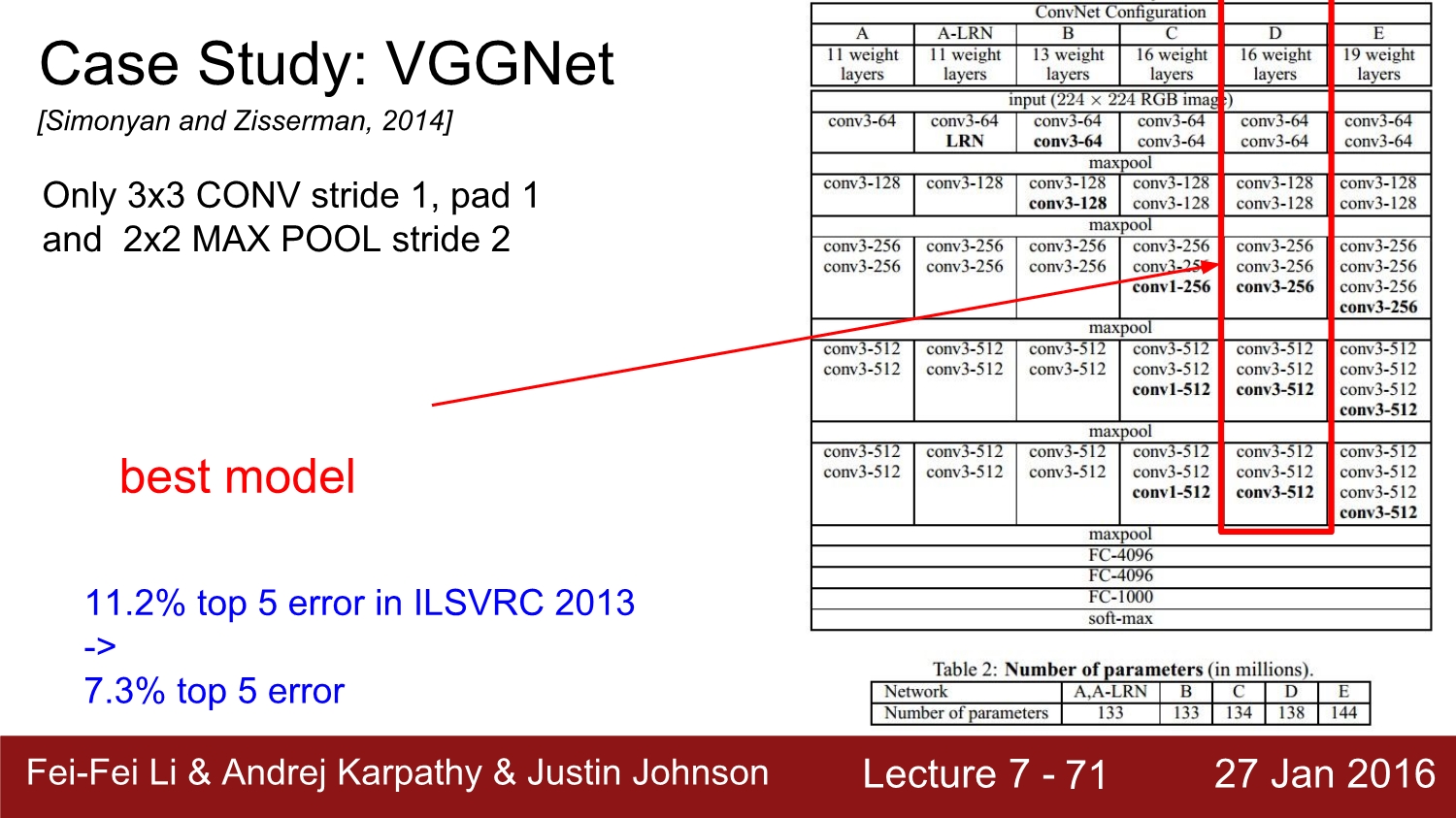
VGG net: https://ys-cs17.tistory.com/6
VGG NET: Very Deep Convolution Networks For Large-Scale Image Recognition
Very Deep Convolution Networks For Large-Scale Image Recognition (VGG16) -Karen Simonyan, Andrew Zisserman- 1. Introduction Faster-RCNN을 분석하기 앞서 여기서 쓰이는 네트워크 모델인 VGG16을 먼저 공..
ys-cs17.tistory.com
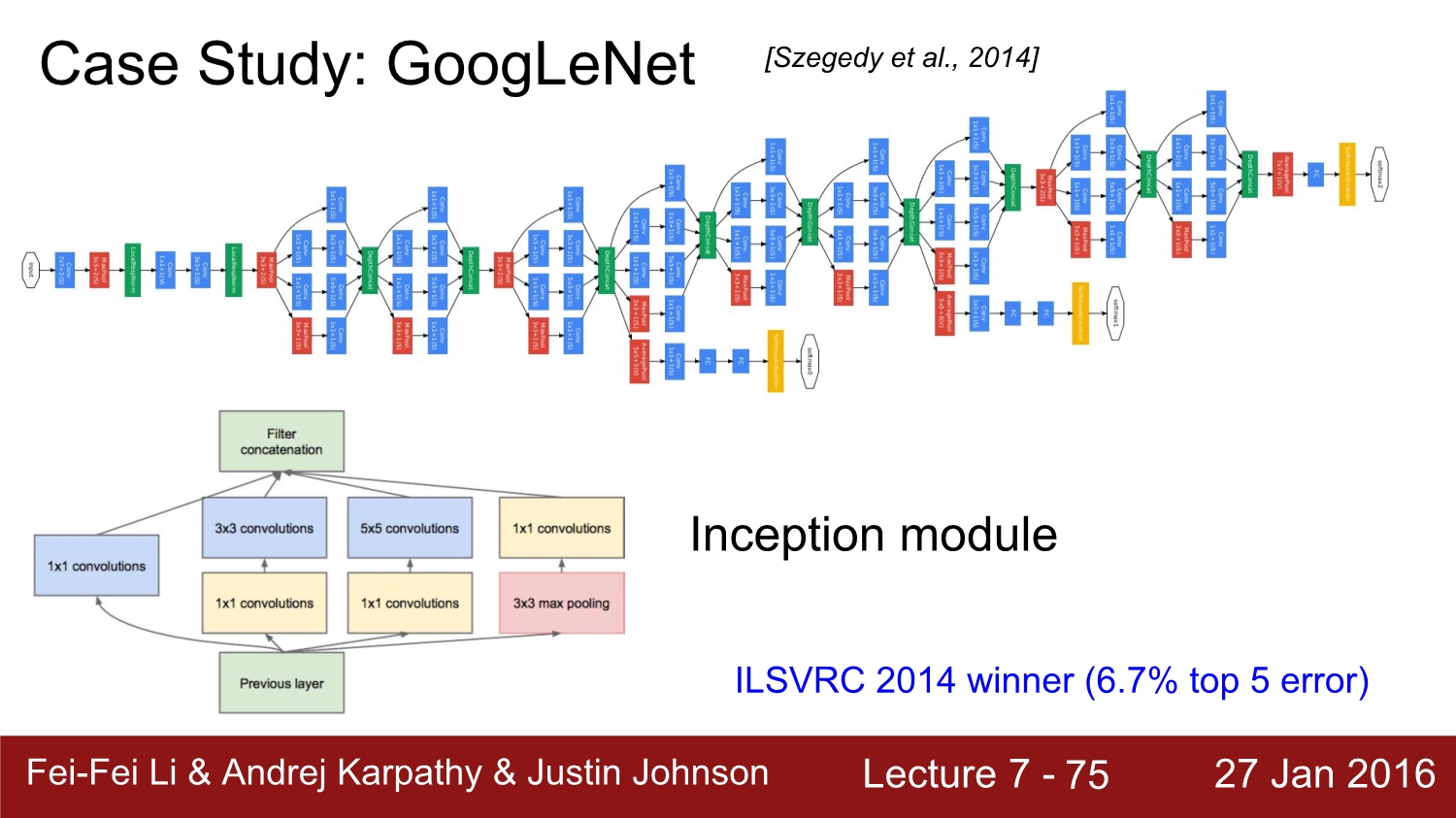
다음은 vgg과 같이 나왔었던 google의 google net이다. 물론 2014년도에 image net에서 1등을 하였지만 위와 같이 구조가 너무 복잡하여 사람들이 vgg를 더욱 선호하였다고 한다.
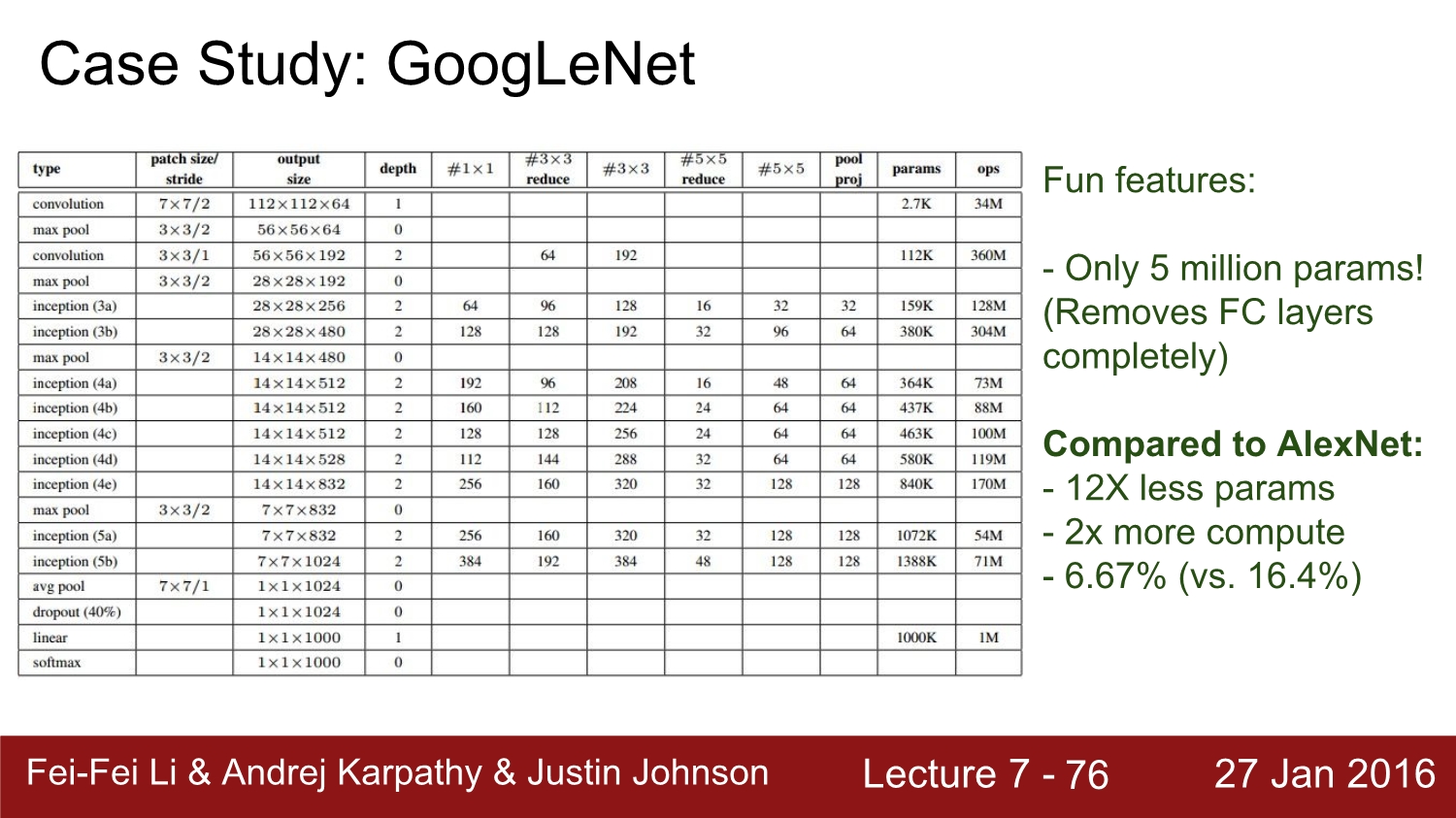
Alex net과 비교를 하면 여기서는 avg layer를 사용한다. 1개의 행을 만듦으로 써 parameter의 size가 매우 작아진다. 총 500여만 개로 줄어들게 되는데 물론 alex net보다 size가 작고, 정확도는 더 높다.

다음은 res net이다. 원래는 res net도 리뷰를 하려고 했지만 그전에 백준 알고리즘과 cs231n을 공부하고 있어서 추후에 리뷰하겠다. res net은 2015년 모든 분야에서 1등을 하였다.

매년 network의 depth는 점점 깊어진다. res net에 같은 경우에는 152개의 layer를 사용한다. depth 뿐만 아니라 loss 또한 매우 줄어든다.
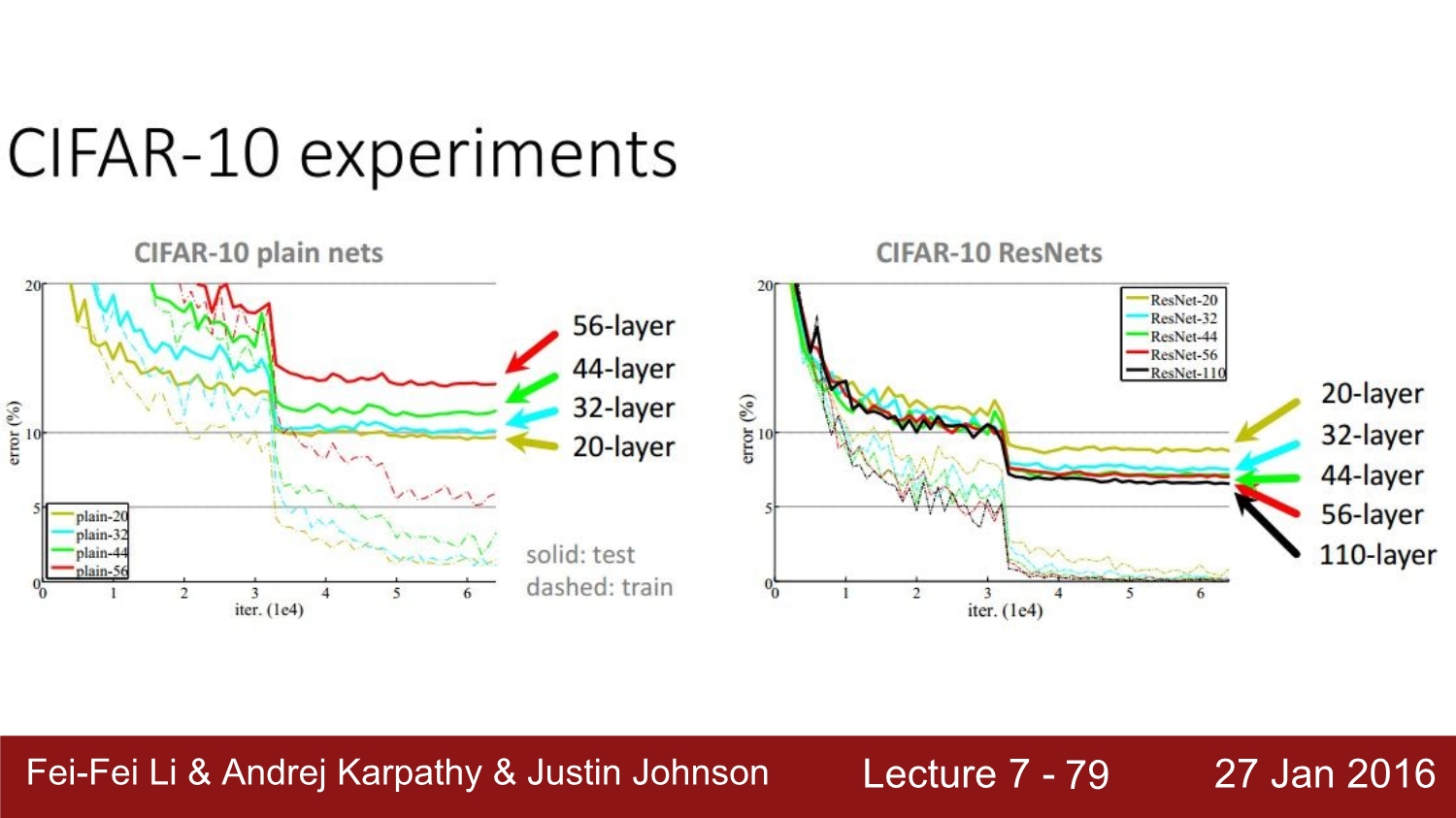
과연 layer의 수가 많아질수록 정확도가 올라갈까? 정답은 x이다. res net 연구진들이 실험을 해본 결과 왼쪽의 그래프처럼 오히려 layer가 많아질수록 loss가 커지는 것을 볼 수 있다. 그 이유는 각각의 layer들이 최적화가 안되어 있기 때문이다. res net의 같은 경우에는 각 layer를 잘 최적화하여 layer가 많아질수록 loss가 줄어드는 모습을 볼 수 있다.
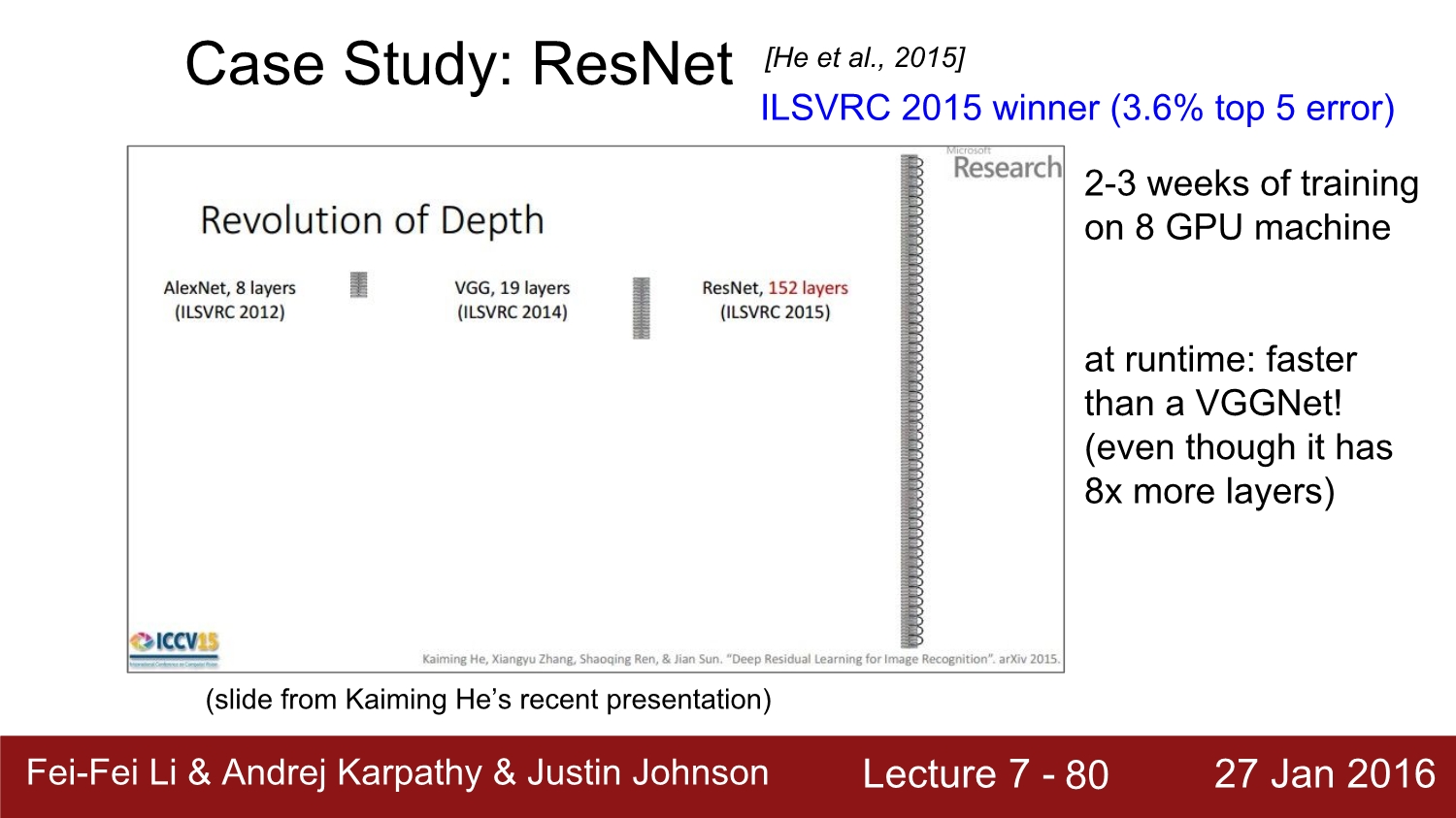
resnet의 같은 경우 치명적인 단점은 train time이 매우 긴 것이다. 아무래도 layer의 수가 매우 많아서 그런 이유가 있다. 연구진들은 8개의 gpu로 2~3주간 train을 했다고 한다. 하지만 test time은 매우 빠르다고 한다.

resnet의 같은 경우 convolution을 거치자마자 pooling을 진행한다 그 후 skip connection이라는 것을 사용한다.
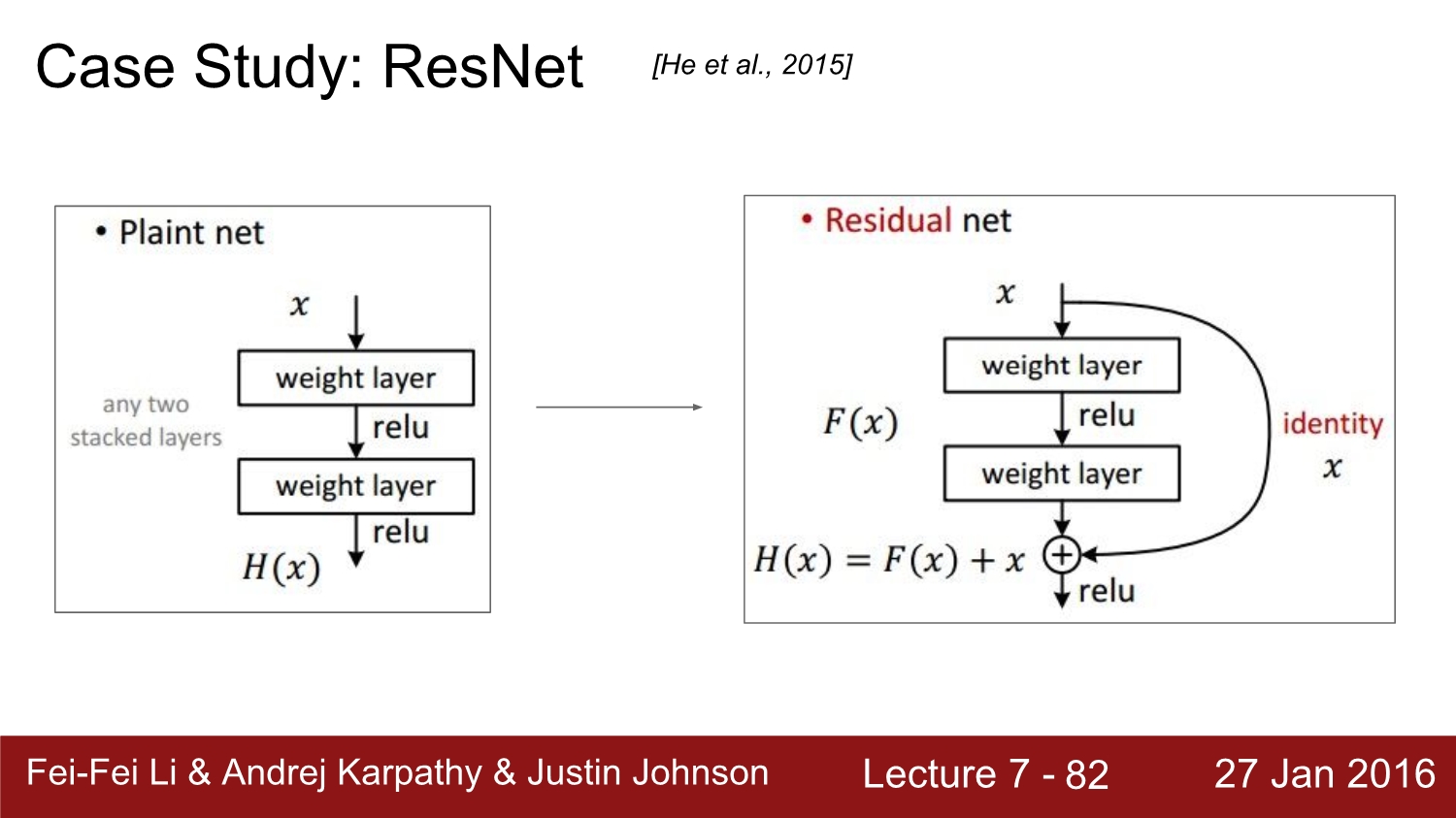
skip connection에 대해 설명을 한 것인데 나중에 res net 논문 리뷰에서 더욱 자세히 설명하겠다. 여기서는 생략한다.

resnet이 잘될 수 있었던 이유는 batch normalization, weight initailization, sgd+momentum, lr를 0.1로 사용, drop out을 사용 안 한 점이 있다.

마지막으로 요약하자면 우리는 layer들의 역할과 기능에 대해 이야기했다. 요즘 트렌드는 더 작은 filter를 사용하여 parameter를 줄이고, depth 한 layer를 사용한다고 한다. 또한 pooling과 fc layer를 사용하지 않는다고 한다. 이 수업은 2016년 기준이니 잘 참고 바란다.
referance
http://cs231n.stanford.edu/2016/
https://www.youtube.com/watch?v=KT4iD6yiqwo
'study > cs231n' 카테고리의 다른 글
| Lecture 9: Understanding and Visualizing Convolutional Neural Networks (0) | 2020.04.21 |
|---|---|
| Lecture 8: Spatial Localization and Detection (0) | 2020.04.17 |
| Lecture 6: Training Neural Networks, Part 2 (0) | 2020.04.13 |
| Lecture 5-2: Training NN part 1 (~Data preprocessing) (0) | 2020.04.13 |
| Lecture 5-1: Training NN part 1 (~activation function) (0) | 2020.04.13 |




